|
The collection processing, interpretation and presentation of
numerical data all belong to the domain of statistics. These
tasks include the calculation of football goals averages,
collecting data on births and deaths, evaluating the
effectiveness of commercial products, and forecasting the
weather. Statistical information is presented to us constantly
on radio and television. Our enthusiasm for statistical facts is
encouraged by national newspapers such as the daily journals and
magazines.
The word "statistics" is used in several ways. It
can refer not only to the mere tabulation of numeric
information, as in reports of stock market transactions, but
also to the body of techniques used in processing or analyzing
data.
The word "statistician" is also used in several
ways. The term can be applied to those who simply collect
information, as well as to those who prepare analyses or
interpretations, and it is also applied to scholars who develop
the mathematical theory on which statistics is based.
In Sections 1.1 and 1.2, we discuss the recent growth of
statistics and its ever widening range of applications. In
Section 1.3 we explain the distinction between the two major
branches of statistics, descriptive statistical inference, and
in the optional Section 1.4 we discuss the nature of various
kinds of data and in connection with this warn the reader
against the indiscriminate mathematical treatment of statistical
data. |
|
1.1 The Growth of Modern Statistics
There are several reasons why the scope of
statistics and the need to study statistics have grown
enormously in the last fifty or so years. One reason is the increasingly quantitative approach employed in
all the sciences as well as in business and many other
activities which directly affect our lives. This includes
the use of mathematical techniques in the evaluation of
anti-pollution control, in inventory planning, in the analysis
of traffic patterns, in the study of the effects of various
kinds of medications, in the evaluation of teaching techniques,
in the analysis of competitive behavior of businessmen and
governments, in the study of diet and longevity, and so forth.
The availability of powerful computers has greatly increased our
ability to deal with numerical information. Many types of
computers are also inexpensive, so that sophisticated
statistical work can be done by small businessmen, college
students, and even high-school students.
The other reason is that the amount of data that
is collected, processed, and disseminated to the public for one
reason or another has increased almost beyond comprehension, and
what part is "good" statistics and what part is "bad" statistics
is anybody's guess. To act as watchdogs, more persons with some knowledge of statistics
are needed to take an active part in the collection of the data,
in the analysis of the data, and what is equally important, in
all of the preliminary planning. Without the latter, it is
frightening to think of all the things that can go wrong in the
compilation of statistical data. The results of costly surveys
can be useless if questions are ambiguous or asked in the wrong
way, if they are asked of the wrong persons, in the wrong place,
or at the wrong time. Much of this is just common sense, as is
illustrated by the following examples:
Example
To determine public sentiment about the continuation of a
certain government program an interviewer asks: "Do you feel
that this wasteful program should be stopped?" Explain why this
will probably not yield the desired information.
Solution:
The interviewer is "begging the question" by suggesting, in
fact, that the program is wasteful.
Example
To study consumer reaction to a new convenience food, a house
to house survey is conducted during week day mornings, with no
provisions for return visits in case no one is home. Explain why
this may well yield misleading information.
Solution:
This survey will fail to reach those who are most likely to
use the product: single persons and married couples with both
spouses employed.
Although much of the above- mentioned growth of statistics
began prior to the "computer revolution," the widespread
availability and use of computers have greatly accelerated the
process. In particular, computers enable us to handle, analyze
and dissect large masses of data, and they enable us to perform
calculations which previously had been too cumbersome even to
contemplate. Our objective in these notes will be your gaining
an understanding of the ideas of statistics. Access to a
computer is not critical for this objective. Computer uses are
occasionally illustrated in these notes, but nearly all the
exercises can be done with nothing more than a four – function
calculator. |
|
1.2 The Study of Statistics
The subject of statistics can be presented at various levels
of mathematical difficulty, and it may be directed toward
applications in various fields of inquiry. Accordingly, many
textbook have been written on business statistics, educational
statistics, medical statistics, psychological statistics … and
even on statistics for historians. Although problems arising in
these various disciplines will sometimes require special
statistical techniques, none of the basic methods discussed in
this text is restricted to any particular field of application.
In the same way in which 2 + 2 = 4 regardless of whether we are
adding dollar amounts, horses, or trees, the methods we shall
present provide statistical models which apply regardless of
whether the data are IQ's, tax payments, reaction times,
humidity readings, test scores, and so on. To illustrate this
further, consider the following situations.
|
1 : |
In a random sample of 200 retired persons, 137
stated that they prefer living in an apartment to living
in a one - family home. At the 0.05 level of
significance does this refute the claim that 60 percent
of all retired persons prefer living in an apartment to
living in a one – family home? |
The question asked here should be clear, and it should also be
clear that the answer would be of interest mainly to social
scientists or to persons in the construction industry. However,
if we wanted to cater to the special interests of students of
biology, engineering education or ecology, we might rephrase the
situation as follows:
|
2 : |
In a random sample of 200 citrus trees exposed
to a 20o frost, 137 showed some damage to
their fruit. At the 0.05 level of significance does this
refute the claim that 60 percent of citrus trees exposed
to a 20o frost will show some damage to their
fruit? |
|
3 : |
In a random sample of 200 transistors made by a
given manufacturer, 137 passed an accelerate performance
test. At the 0.05 level of significance does this refute
the claim that 60 percent of all transistors made by a
given manufacturer will pass the test? |
|
4 : |
In a random sample of 200 high school seniors in
a large city, 137 said that they will go on to college.
At the 0.05 level of significance does this refute the
claim that 60 percent of all high school seniors in a
large city will go to college? |
|
5 : |
In a random sample of 200 cars tested for the
emission of pollutants, 137 failed to meet a state's
legal standards. At the 0.05 level of significance does
this refute the claim that 60 percent of all cars tested
in this state will fail to meet legal emission
standards? |
So far as the work in these notes is concerned, the
statistical treatment of all these versions is the same, and
with some imagination the reader should be able to rephrase it
for virtually any field of specialization. As some authors do,
we could present, and so designate, special problems for readers
with special interests, but this would defeat our goal of
impressing upon the reader the importance of statistics in all
of science, business, and everyday life. To attain this goal we
have included in this text exercises covering a wide spectrum of
interests.
To avoid the possibility of misleading anyone with our various
versions, let us make it clear that we cannot squeeze all
statistical problems into the same mold. Although the methods we
shall study in these notes are all widely applicable, it is
always important to make sure that the statistical model we are
using is the right one.
|
|
1.3 Descriptive Statistics and
Statistical Inference
The origin of modern statistics can be traced to
two areas of interest which, on the surface have very little in
common: government (political science), and games of chance.
Governments have long used census data to count
persons and property, and the problem of describing, summarizing
and analyzing census data has led to the development of methods
which, until recently, constituted about all there was to the
subject of statistics.
These methods, which at first consisted primarily of
presenting data in the form of tables and charts, make up what
we now call descriptive statistics. This includes anything
done to data which is designed to summarize or describe, without
going any further; that is, without attempting to infer anything
that goes beyond the data, themselves. For instance, if tests
performed on six small cars imported in 1986 showed that they
were able to accelerate from 0 to 60 miles per hour in 18.7,
19.2, 16.2, 12.3, 17.5, and 13.9 seconds, and we report that
half of them accelerated from 0 to 60 mph in less than 17.0
seconds, our work belongs to the domain of descriptive
statistics. This would also be the case if we claim that these
six cars averaged
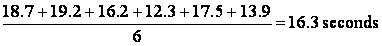
But is not if we conclude that half of all cars imported that
year could accelerate from 0 to 60 mph in less than 17.0
seconds.
Although descriptive statistics is an important
branch of statistics and it continues to be widely used,
statistics information usually arises from samples (from
observations made on only part of a large set of items), and
this means that its analysis requires generalizations which go
beyond the data.
As a result, the most important feature of the recent growth of
statistics has been a shift in emphasis from methods which
merely describe to methods which serve to make generalizations;
that is, a shift in emphasis from descriptive statistics to the
methods of statistical inference.
Such methods are required, for instance, to predict the
operating life span of a hand – held calculator (on the basis of
the performance of several such calculators);to estimate the
1995 assessed value of all privately owned property in Cairo (on
the basis of business trends, population projections, and so for
the); to compare the effectiveness of two reducing diets (on the
basis of the weight losses of persons who have been on the
diets); to determine the most effective dose of a new medication
(on the basis of tests performed with volunteer patients from
selected hospitals); or to predict the flow of traffic on a
freeway which has not yet been built (on the basis of past
traffic counts on alternative routes).
In each of the situations described in the
preceding paragraph, there are uncertainties because there is
only partial, incomplete, or indirect information; therefore,
the methods of statistical inference are needed to judge the
merits of our results, to choose a "most promising" prediction,
to select a "most reasonable" (perhaps, a "potentially most
profitable") course of action.
In view of the uncertainties, we handle problems like these
statistical methods which find their origin in games of chance.
Although the mathematical study of games of chance dates to the
seventeenth century, it was not until the early part of the
nineteenth century that the theory developed for "heads or
tails," for example, or "red or black" or even or odd," was
applied also to real-life situations where the outcomes were
"boy or girl," "life or death," "pass or fail," and so forth.
Thus, probability theory was applied to many problems in the
behavioral, natural, and social sciences, and nowadays it
provides an important tool for the analysis of any situation (in
science, in business, or in everyday life) which in some way
involves an element of uncertainty of chance. In particular, it
provides the basis for the methods which we use when we
generalize from observed data, namely, when we use the methods
of statistical inference.
In recent years, it has been suggested that the
emphasis has swung too far from descriptive statistics to
statistical inference, and that more attention should be paid to
the treatment of problems requiring only descriptive techniques. To accommodate these needs, some new descriptive
methods have recently been developed under the general heading
of exploratory data analysis. Two of these will be presented. |
|
1.4 The Nature of Statistical Data
Statistical data are the raw material of
statistical investigations – they arise whenever measurements
are made or observations are recorded.
They may be weights of animals, measurements of
personality traits, or earthquake intensities, and they may be
simple "yes or no" answer or descriptions of persons' marital
status as single, married, widowed, or divorced. Since we said that statistics deals with
numerical data, this requires some explanation, because "yes or
no" answers and descriptions of marital status would hardly seem
to qualify as being numerical. Observe, however, that we can
record "yes or no" answers to a question as 0 (or as 1 and 2, or
perhaps as 29 and 30 if we are referring to the 15th
"yes or no" question of a test), and that we can record a
person's marital status as 1, 2, 3, or 4, depending on whether
the person is single, married, widowed, or divorced. In this
artificial or nominal way, categorical (qualitative or
descriptive) data can be made into numerical data, and if we
thus code the various categories, we refer to the numbers we
record as nominal data.
Nominal data are numerical in name only, because
they do not share any of the properties of the numbers we deal
with in ordinary arithmetic. For instance, if we record marital status as 1, 2, 3, or 4, as
suggested above, we cannot write 3 > 1 or 2,4, and we cannot
write 2 - 1 = 4 - 3, 1 + 3 = 4, or 4
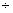 2
= 2. It is important, therefore, always to check whether
mathematical calculations performed in a statistical analysis
are really legitimate. 2
= 2. It is important, therefore, always to check whether
mathematical calculations performed in a statistical analysis
are really legitimate.
Let us now consider some examples where data share some, but
not necessarily all, of the properties of the numbers we deal
with in ordinary arithmetic. For instance, in mineralogy the
hardness of solids is sometimes determined by observing "what
scratches what." If one mineral can scratch another it receives
a higher hardness number, and on Mohs' scale the numbers form 1
to 10 are assigned, respectively, to talc, gypsum, calcite,
fluorite apatite, feldspar, quartz, topaz, sapphire, and
diamond. With these numbers, we can write 6 > 3, for Example or
7 < 9, since feldspar is harder than calcite and quartz is
softer than sapphire. On the other hand, we cannot write 10 - 9
= 2 -1, for Example because the difference in hardness between
diamond and sapphire is actually much greater than that between
gypsum and talc. Also, it would be meaningless to say that topaz
is twice as hard as fluorite simply because their respective
hardness numbers on Mohs' scale are 8 and 4.
If we cannot except set up inequalities
as was the case in the proceeding example, we refer to the
data as ordinal data. In connection with ordinal data > does
not necessarily mean "greater than" it may be used to denote
"happier than," "preferred to," "more difficult than," "tastier
than," and so forth.
If we can also form differences, but not multiply
or divide, we refer to the data as interval data.
To give an example, suppose we are given the following
temperature readings Fahrenheit "63o, 67o,
91o, 107o, 126o, and 131o."
Here, we can write 107 o is warmer than 68 o
and that 91o is colder than 131o. Also, we
can write 68 o-63o = 131o - 126o,
since equal temperature differences are equal in the sense that
the same amount of heat is required to raise the temperature of
an object from 63o to 68 o as from 126o
to 131o. On the other hand, it would not mean
much if we say that 126 o is twice as hot as 63o,
even though 126 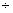 63
= 2. To show why, we have only to change to the Celsius scale,
where the first temperature becomes 63
= 2. To show why, we have only to change to the Celsius scale,
where the first temperature becomes
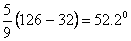 , ,
the
second temperature becomes
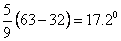 , ,
and
the first figure is now more than three times the second. This
difficulty arises because the Fahrenheit and Celsius scales both
have artificial origins (zeros); in other words, the number 0 of
neither scale is indicative of the absence of whatever quantity
we are typing to measure.
If we can also form quotients, we refer to the
data as ratio data, and such data are not difficult to find.
They include all the usual measurements (or determinations) of
length, height, money amounts, weight, volume, area, pressure,
elapsed time (though not calendar time), sound intensity,
density, brightness, velocity, and so on.
The distinction we have made here between nominal,
ordinal, interval, and ratio data is important, for as we shall
see, the nature of a set of data may suggest the use of
particular statistical techniques. To emphasize the point that what we can and cannot do
arithmetically with a given set of data depends on the nature of
the data, consider the following scores which four students
obtained in the three parts of a comprehensive history test.
|
Students |
Tests |
|
|
A |
B |
C |
Total |
|
L
T
H
R |
89
61
40
13 |
51
56
70
77 |
40
54
55
72 |
180
171
183
162 |
The totals for the four students are 180, 171, 165, and 162,
so that L scored highest, followed by T, H, and R.
Suppose now that somebody proposes that we compare the overall
performance of the four students by ranking their scores from
high to low for each part of the test, and then average their
ranks. What we get is shown in the following table:
|
|
A |
B |
C |
Average Rank |
|
L |
1 |
4 |
4 |
3 |
|
T |
2 |
3 |
3 |
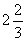
|
|
H |
3 |
2 |
2 |
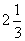
|
|
R |
4 |
1 |
1 |
2 |
Here L's average rank was calculated as
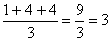
, T's as,
and so forth.
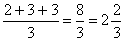
Now, if we look at the average ranks, we find that R came out
best, followed by H, T, and L, so that the order has been
reversed from what it was before. How can this be? Well, strange
things can happen when we average ranks. For instance, when it
comes to their ranks, L's outscoring T by 28 points in counts
just as much as T's outscoring her by 5 points in B, and T's
outscoring H by 21 points in A counts just as much as H's
outscoring him by a single point in C. We conclude that,
perhaps, we should not have averaged the ranks, but it might
also be pointed out that, perhaps, we should not even have
totaled the original scores. The variation of A scores, which go
from 13 to 89, is much greater than that of other two kinds of
scores, and this strongly affects the total scores and suggests
a possible shortcoming of the procedure. We shall not go into
this here, as it has been our goal merely to alert the reader
against the indiscriminate use of statistical techniques. |
|
|
|
|