2.1 Introduction
In Chapter 1, we briefly introduced the concept of statistical
inference-the process of inferring information about a
population from a sample. Because information about populations
can usually be described by parameters, the statistical
technique used generally deals with drawing inferences about
population parameters from sample statistics. (Recall that a
parameter is a measurement about a population, and a statistic
is a measurement about a sample.)
Working within the covers of a statistics
textbook, we can assume that population parameters are known. In
real life, however, calculating parameters become prohibitive
because populations tend to be quite large. As a result, most
population parameters are unknown.
For example, in order to determine the mean annual income of
blue-collar workers, we would have to ask each blue-collar
worker what his or her income is and then calculate the mean of
all the responses. Because this population consists of several
million people, the task is both expensive and impractical. If
we are willing to accept less than 100% accuracy, we can use
statistical inference to obtain an estimate.
Rather than investigating the entire population,
we select a sample of workers, determine the annual income of
the workers in this group, and calculate the sample mean. While
there is very little chance that the sample mean and the
population mean are identical, we would expect them to be quite
close. However, for the purposes of statistical inference, we
need to be able to measure how close the sample mean is likely
to be to the population mean. In this chapter, however, we will discuss the basic concepts and
techniques of sampling itself. But first we will take a look at
various sources for collecting data. |
|
2.2 Sources of Data
The validity of the results of a statistical
analysis clearly depends on the reliability and accuracy of the
data used. Whether you are actually involved in collecting the
data; performing a statistical analysis on the data, or simply
reviewing the results of such an analysis, it is important to
realize that the reliability and accuracy of the data depend on
the method of collection.
Three of the most popular sources of statistical
data are published data, data collected from observational
studies, and data collected from experimental studies.
2.2.1 Published Data
The use of published data is often preferred due
to its convenience, relatively low cost, and reliability
(assuming that it has been collected by a reputable
organization). There is an enormous amount of published
data produced by government agencies and private organizations,
available in printed form, on data tapes and disks, and
increasingly on the Internet. Data published by the same
organization that collected them are called primary data.
An Example of primary data would be the data published by Egypt
Bureau of the Census, which collects data on numerous industries
as well as conducts the census of the population every ten
years. Statistics agency is the central statistical agency,
collecting data on almost every aspect of social and economic
life in the country. These primary sources of information are
invaluable to decision makers in both the government and private
sectors.
Secondary data refers to data that are published
by an organization different from the one that originally
collected and published the data.
A popular source of secondary data is The Statistical Book of
Egypt, which compiles data from several primary government
sources and is updated annually. Another Example of a secondary
data source is Central Bank which has a variety of financial
data tapes that contain data compiled from such primary sources
as the Stock Exchange. Care should be taken when using secondary data,
as errors may have been introduced as a result of the
transcription or due to misinterpretation of the original
terminology and definitions employed.
An interesting Example of the importance of knowing how data
collection agencies define their terms appeared in an article in
The Globe and Mail (February 12, 1996). The United States
and Canada had similar unemployment rates up until the 1980s, at
which time Canada's rate started to edge higher than the U.S.
rate. By February 1996, the gap had grown to almost four
percentage points (9.6% in Canada compared with 5.8% in the
United States). Economists from the United States and Canada met
for two days to compare research results and discuss possible
reasons for this puzzling gap in jobless rates. The conference
organizer explained that solving this mystery matters because
"we have to understand the nature of unemployment to design
policies to combat it." An Ohio State University economist was
the first to notice a difference in how officials from the two
countries define unemployment. "If jobless people say they are
searching for work, but do nothing more than read job
advertisements in the newspaper, Canada counts them as
unemployed. U.S. officials dismiss such 'passive' job hunters
and count them as being out of the labor force altogether, so
they are not counted among the jobless." Statistics Canada
reported that this difference in definitions accounted for
almost one-fifth of the difference between the Canadian and U.S.
unemployment rates.
2.2.2 Observational and Experimental
Studies
If relevant data are not available from published
sources, it may be necessary to generate the data by conducting
a study. This will especially be the case when data are needed
concerning a specific company or situation. The difference between two important types of studies –
observational and experimental – is best illustrated by means of
an example.
Example (1)
Six months ago, the director of human resources for a large
mutual fund company announced that the company had arranged for
its salespeople to use a nearby fitness center free of charge.
The director believes that fitter salespeople have more energy
and an improved appearance, resulting in higher productivity.
Interest and participation in the fitness initiative were high
initially, but after a few months had passed, several employees
stopped participating. Those who continued to exercise were
committed to maintaining a good level of fitness, using the
fitness center about three times per week on average.
The director recently conducted an observational study and
determined that the average sales level achieved by those who
regularly used the fitness center exceeded that of those who did
not use the center. The director was tempted to use the
difference in productivity levels to justify the cost to the
company of making the fitness center available to employees. But
the vice-president of finance pointed out that the fitness
initiative was not necessarily the cause of the
difference in productivity levels. Because the salespeople who
exercised were self-selected - they determined themselves
whether or not to make use of the fitness center-it is quite
likely that the salespeople who used the center were those who
were more ambitious and disciplined. These people would probably
have had higher levels of fitness and productivity even without
the fitness initiative. We therefore cannot necessarily conclude
that fitness center usage led to higher productivity. It may be
that other factors, such as ambition and discipline, were
responsible both for higher fitness center usage and higher
productivity.
The director and vice-president then discussed the possibility
of conducting an experimental study, designed to control
which salespeople made regular use of the fitness center. The
director would randomly select 60 salespeople to participate in
the study. Thirty of these would be randomly selected and
persuaded to use the fitness center on a regular basis for six
months. The other 30 salespeople selected would not be
approached, but simply would have their sales performances
monitored along with those using the fitness center regularly.
Because these two groups were selected at random, we would
expect them to be fairly similar in terms of original average
fitness level, ambition, discipline, age, and other factors that
might affect performance. From this experimental study, we would
be more confident that any significantly higher level of
productivity by the group using the fitness center regularly
would be due to the fitness initiative rather than other
factors.
The point of the preceding Example is to
illustrate the difference between observational study and an
experimental (or controlled) study. In the observational study,
a survey simply was conducted to observe and record the average
level for each group, without attempting to control any of the
factors that might influence the sales levels. In the
experimental study, the director controlled one factor (regular
use of the fitness center) by randomly selecting who
would be persuaded to use the center regularly, thereby reducing
the influence of other factors on the difference between the
sales levels of the two groups.
Although experimental studies make it easier to
establish a cause–and–effect relationship between two variables,
observational studies are used predominately in business and
economics.
More often than not, surveys are conducted to collect business
and economic data (such as consumer preferences or unemployment
statistics), with no attempt to control any factors that might
affect the variable of interest.
Surveys
One of the most familiar methods of
collecting primary data is the survey, which solicits
information from people concerning such things as their income,
family size, and opinions on various issues.
We're all familiar, for example, with opinion that accompany
each political election. The Gallup poll and the Harris survey
are two well-known surveys of public opinion
whose results are often reported in the media. But the
majority of surveys are conducted for private use.
Private surveys are used extensively by market
researchers to determine the preferences and attitudes of
consumers and voters. The results can be used for a variety
of purposes, from helping to determine the target market
for an advertising campaign to modifying a candidate's platform
in an election campaign. As an illustration, consider a
television network that has hired a market research firm to
provide the network with a profile of owners of luxury
automobiles, including what they watch on television and at what
times. The network could then use this information to develop a
package of recommended time slots for Cadillac
commercials including costs; that it would present to
General Motors. It is quite likely that many, students reading
this notes will one day be marketing executives who will "live
and die" by such market research data.
Many researchers feel that the best way to survey people is by
means of a personal interview, which involves an interviewer
soliciting information from respondent by asking prepared
questions. A personal interview has the
advantage of having a higher expected response rate than other
methods of data collection. In addition, there will probably be
fewer incorrect responses resulting from respondents
misunderstanding some questions, because the interviewer can
clarify misunderstandings when asked to. But the interviewer
must also be careful not to say too much, for fear of biasing
the response. To avoid introducing such biases, as well as to
reap the potential benefits of a personal interview, interviewer
must be well trained in proper interviewing techniques and well
informed on the purpose of the study. The main disadvantage of
personal interviews is that they are expensive, especially when
travel is involved. A telephone interview is usually less
expensive, but it is also less personal and has a lower expected
response rate.
A third popular method of data collection is the self -
administered questionnaire, which is usually mailed
to a sample of people selected to be surveyed. This is a
relatively inexpensive method of conducting a survey and is
therefore attractive when the number of people to be surveyed is
large. But self-administered questionnaires usually have a low
response and may have a relatively high number of incorrect
responses due to respondents misunderstanding some questions.
Whether a questionnaire is self – administered or completed by
an interviewer, it must be well designed. Proper questionnaire
design takes knowledge, experience, time, and money. Some
basic points to consider regarding questionnaire design follow.
1-
First and foremost, the questionnaire
should be kept as short as possible to encourage respondents
to complete it. Most people are unwilling to spend much time
filling out a questionnaire.
2-
The questions themselves should also be short, as
well as simply and clearly worded, to enable respondents to answer quickly,
correctly, and without ambiguity. Even familiar terms, such as
"unemployed" and "family," must be defined carefully because
several interpretations are possible.
3-
Questionnaires often begin with simple demographic
questions to help respondents get started and become
comfortable quickly.
4-
Dichotomous questions
(questions with only two possible responses, such as "yes" and
"no') and multiple – choice questions are useful and
popular because of their simplicity, but they, too, have
possible shortcomings. For example, a respondent's choice of yes
or no to a question may depend on certain assumptions not stated
in the question. In the case of a multiple- choice question, a
respondent may feel that none of the choices offered is
suitable.
5-
Open-ended questions
provide an opportunity for respondents to express opinions more
fully, but they are time-consuming and more difficult to
tabulate and analyze.
6-
Avoid using leading questions,
such as "Wouldn't you agree that the statistics exam was too
difficult?" These types of questions tend to lead the respondent
to a particular answer.
7-
Time permitting,
it is useful to pretest a questionnaire on a small number of
people in order to uncover potential problems, such as ambiguous
wording.
8-
Finally, when preparing the
questions, think about how you intend to tabulate and analyze
the responses. First determine whether you are soliciting
values (i.e., responses) for a qualitative variable or a
quantitative variable. Then consider which type of statistical
techniques – descriptive or inferential – you intend to apply to
the data to be collected, and note the requirements of the
specific techniques to be used. Thinking about these
questions will help to assure that the questionnaire is designed
to collect the data you need.
Whatever method is used to collect primary data, we need to know
something about sampling, the subject of the next section. |
|
2.3 Sampling
The chief motive for examining a sample rather
than a population is cost. Statistical inference permits us to draw conclusions about
a population parameter based on a sample that is quite small in
comparison to the size of the population. For example,
television executives want to know the proportion of television
viewers who watch a network's programs. Because 100 million
people may be watching television in the world on a given
evening, determining the actual proportion of the population
that is watching certain programs is impractical and
prohibitively expensive. The ratings provide approximations of
the desired information by observing what is watched by a sample
of 1,000 television viewers. The proportion of households
watching a particular program can be calculated for the
households in the sample. This sample proportion is then used as
an estimate of the proportion of all households (the population
proportion) that watched the program.
Another illustration of sampling can be taken from
the field of quality control. In order to ensure that a production process is
operating properly, the operations manager needs to know what
proportion of items being produced is defective. If the quality
- control technician must destroy the item in order to determine
whether it is defective, then there is no alternative to
sampling: a complete inspection of the product population would
destroy the entire output of the production process.
We know that the sample proportion of television viewers or of
defective items is probably not exactly equal to the population
proportion we want to estimate. Nonetheless, the sample
statistic can come quite close to the parameter it is designed
to estimate if the target population (the population about which
we want to draw inferences) and the sampled population (the
actual population from which the sample has been taken) are the
same. In practice, these may not be the same. |
|
2.4 Sampling Plans
Our objective in this section is to introduce three different
sampling plans: simple random sampling, stratified random
sampling, and cluster sampling. We begin our presentation with
the most basic design.
2.4.1 Simple Random Sampling
Simple Random Sample
A simple random sample is a sample selected in
such a way that every possible sample with the same number of
observations is equally likely to be chosen.
One way to conduct a simple random sample is to
assign a number to each element in the population,
write these numbers on individual slips of paper, toss them into
a hat, and draw the required number of slips (the sample size,
n) from the hat. This is the kind of procedure that
occurs in raffles, when all the ticket stubs go into a large,
rotating drum from which the winners are selected.
Sometimes the elements of the population are
already numbered.
For example, virtually all adults have Social Security numbers or
Social Insurance numbers; all employees of large corporations
have employee numbers; many people have driver's license
numbers, medical plan numbers, student numbers, and so on. In
such cases, choosing which sampling procedure to use is simply a
matter of deciding how to select from among these numbers.
In other cases, the existing form of numbering has built-in
flaws that make it inappropriate as a source of samples. Not
everyone has a phone number, for example, so the telephone book
does not list all the people in a given area. Many households
have two (or more) adults, but only one phone listing. Couples
often list the phone number under the man's name, so telephone
listings are likely to be disproportionately male. Some people
do not have phones, some have unlisted phone numbers, and some
have more than one phone; these differences mean that each
element of the population does not have an equal probability of
being selected.
After each element of the chosen population has
been assigned a unique number, sample numbers can be selected at
random. A random - number table can be used to select these
sample numbers.
Alternatively, we can employ a software package to generate
random numbers. Both Minitab and Excel have this capability.
Example (2)
A government income-tax auditor has been given responsibility
for 1,000 returns. A computer is used to check the
arithmetic of each return. However, to determine if the returns
have been completed honestly, the auditor must check each entry
and confirm its veracity. Because it takes, on average, one hour
to completely audit a return and she has only one week to
complete the task, the auditor has decided to randomly select 40
returns. The returns are numbered from 1 to 1,000.
Use a computer random -number generator to select the sample for
the auditor.
Solution:
There are several software packages that can produce the
random numbers we need. Minitab and Excel are two of these.
Minitab Output for Example (2)
|
173
259
312
811
654 |
184
544
183
480
859 |
953
588
271
984
478 |
896
754
587
991
633 |
82
870
922
100
157 |
388
700
759
367
470 |
232
893
929
655
615 |
962
690
526
877
32 |
391
320
112
59
258 |
95
28
43
642
887 |
We generated 50 numbers between 1 and 1,000 and stored them in
column 1. Although we needed only 40 random numbers, we
generated 50 numbers because it is likely that some of them will
be duplicated. We will use the first 40 unique random number to
select our sample.
Excel Output for Example (2)
|
165
504
160
832
544 |
78
545
357
661
622 |
120
578
44
426
830 |
987
820
971
173
382 |
705
147
269
909
198 |
827
276
517
973
830 |
725
237
711
856
700 |
466
764
721
813
256 |
759
85
192
152
210 |
361
528
926
915
621 |
We generated 50 numbers between 1 and 1,000 and stored them in
column 1. Although we needed only 40 random numbers, we
generated 50 numbers because it is likely that some of them will
be duplicated. We will use the first 40 unique random number to
select our sample.
Stratified Random Sampling
In making inferences about a population, we
attempt to extract as much information as possible from a
sample. The basic sampling plan, simple random sampling, often
accomplishes this goal at low cost. Other methods, however, can
be used to increase the amount of information about the
population. One such procedure is stratified random sampling.
Stratified Random Sample
A stratified random sample is obtained by
separating the population into mutually exclusive sets, or
strata, and then drawing simple random sample from each stratum.
Examples of criteria for separating a population into strata
(and of the strata themselves) follow.
1 - Sex
Male
Female
2 - Age
Under 20
20-30
31-40
41-50
51-60
Over
60
3 - Occupation
Professional
Clerical
Blue-collar other
4 - Household income
Under $15,000 $15,000-$29,999
$30,000-$50,000
Over
$50,000
To illustrate, suppose a public opinion survey is to be
conducted in order to determine how many people favor a tax
increase. A stratified random sample could be obtained by
selecting a random sample of people from each of the four income
groups described above. We usually stratify in a way that
enables us to obtain particular kinds of information. In this
example, we would like to know if people in the different income
categories differ in their opinions about the proposed tax
increase, since the tax increase will affect the strata
differently. We avoid stratifying when there is no connection
between the survey and the strata. For example, little purpose
is served in trying to determine if people within religious
strata have divergent opinions about the tax increase.
One advantage of stratification is that, besides
acquiring information about the entire population, we can also
make inferences within each stratum or compare strata. For instance, we can estimate what proportion of
the lowest income group favors the tax increase, or we can
compare the highest and lowest income groups to determine if
they differ in their support of the tax increase.
Any stratification must be done in such a way that
the strata are mutually exclusive: each member of the population
must be assigned to exactly one stratum.
After the population has been stratified in this
way, we can employ simple random sampling to generate the
complete sample. There are several ways to do this. For example, we can draw random samples from each
of the four income groups according to their proportions in the
population. Thus, if in the population the relative frequencies
of the four groups are as listed below, our sample will be
stratified in the same proportions. If a total sample of 1,000
is to be drawn, we will randomly select 250 from stratum 1,400
from stratum 2,300 from stratum 3, and 50 from stratum 4.
|
Stratum |
Income Categories |
Population Proportions |
|
1 |
under $15,000 |
25% |
|
2 |
15,000-29,999 |
40 |
|
3 |
30,000-50,000 |
30 |
|
4 |
over 50,000 |
5 |
The problem with this approach, however, is that if we want to
make inferences about the last stratum, a sample of 50 may be
too small to produce useful information. In such cases, we
usually increase the sample size of the smallest stratum (or
strata) to ensure that the sample data provide enough
information for our purposes. An adjustment must then be made
before we attempt to draw inferences about the entire
population. This procedure is beyond the level of these notes.
We recommend that anyone planning such a survey consult an
expert statistician or a reference book on the subject. Better
still, become an expert statistician yourself by taking
additional statistics courses.
2.4.2 Cluster Sampling
Cluster Sample
A cluster sample is a simple random sample of
groups or clusters of elements.
Cluster sampling is particularly useful when it is
difficult or costly to develop a complete list of the population
members (making it difficult and costly to generate a simple
random sample). It is also useful whenever the population
elements are widely dispersed geographically.
For example, suppose we wanted to estimate the average annual
household income in a large city. To use simple random sampling,
we would need a complete list of households in the city from
which to sample. To use stratified random sampling, we would
need the list of households, and we would also need to have each
household categorized by some other variable (such as age of
household head) in order to develop the strata. A less expensive
alternative would be to let each block within the city represent
a cluster. A sample of clusters could then be randomly selected,
and every household within these clusters could be questioned to
determine income. By reducing the distances the surveyor must
cover to gather data, cluster sampling reduces the cost.
But cluster sampling also increases sampling
error,
because households belonging to the same cluster are likely to
be similar in many respects, including household income. This
can be partially offset by using some of the cost savings to
choose a larger sample than would be used for a simple random
sample.
Sample Size
Whichever type of sampling plan you select, you still have to
decide what size of sample to use. In determining the
appropriate sample size, we can rely on our intuition, which
tells us that the larger the sample size is, the more accurate
we can expect the sample estimates to be. |
|
2.5 Errors Involved in Sampling
Two major types of errors
can arise when a sample of observations is taken from a
population: sampling error and nonsampling error.
Managers reviewing the results of sample surveys and studies, as
well as researchers, who conduct the surveys and studies, should
understand the sources of these errors.
Sampling Error
Sampling error refers to differences between the
sample and the population that exist only because of the
observations that happened to be selected for the sample. Sampling error is an error that we expect to
occur when we make a statement about a population that is based
only on the observations contained in a sample taken from the
population. To illustrate, consider again the Example
described in which we wish to determine the mean annual income
of blue-collar workers. As was stated there, we can use
statistical inference to estimate the mean income
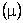 of
the population if we are willing to accept less than 100%
accuracy. If we record the incomes of a sample of the workers
and find the mean of
the population if we are willing to accept less than 100%
accuracy. If we record the incomes of a sample of the workers
and find the mean 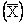 of
this sample of incomes, this sample mean is an estimate of the
desired population mean. But the value of of
this sample of incomes, this sample mean is an estimate of the
desired population mean. But the value of
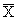 will
deviate from the population mean will
deviate from the population mean
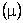 simply
by chance, because the value of the sample mean depends on which
incomes just happened to be selected for the sample. The
difference between the true (unknown) value of the population
mean simply
by chance, because the value of the sample mean depends on which
incomes just happened to be selected for the sample. The
difference between the true (unknown) value of the population
mean 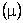 and
its sample estimate and
its sample estimate 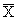 is
the sampling error. The size of this deviation may be large
simply due to bad luck that a particularly unrepresentative
sample happened to be selected. The only way we can reduce the
expected size of this error is to take a larger sample. is
the sampling error. The size of this deviation may be large
simply due to bad luck that a particularly unrepresentative
sample happened to be selected. The only way we can reduce the
expected size of this error is to take a larger sample.
Given a fixed sample size, the best we can do is to state the
probability that the sampling error is less than a certain
amount. It is common today for such a statement to accompany the
results of an opinion poll. If an opinion poll states that,
based on sample results, Candidate Kreem has the support of 54%
of eligible voters in an upcoming election, that statement may
be accompanied by the following explanatory note: This
percentage is correct to within percentage points, 29 times out
of 30. This statement means that we have a certain level of
confidence (95%) that the actual level of support for Candidate
Kreem is between 51 % and 57%.
Nonsampling Error
Nonsampling error is more serious than sampling
error,
because taking a larger sample won't diminish the size, or
the possibility of occurrence, of this error. Even a census
can (and probably will) contain nonsampling errors. Nonsampling
errors are due to mistakes made in the acquisition of data or
due to the sample observations being selected improperly.
Three Types of Nonsampling Errors
1- Errors in Data Acquisition.
These types of errors arise from the recording of incorrect
responses. This may be the result of incorrect measurements
being taken because of faulty equipment, mistakes made during
transcription from primary sources, inaccurate recording of data
due to misinterpretation of terms, or inaccurate responses to
questions concerning sensitive issues such as sexual activity or
possible tax evasion.
2- Nonresponse Error.
Nonresponse error refers to error (or bias) introduced when
responses are not obtained from some members of the sample. When this happens, the sample observations that are collected
may not be representative of the target population, resulting in
biased results. Nonresponse can occur for a number of reasons.
An interviewer may be unable to contact a person listed in the
sample, or the sampled person may refuse to respond for some
reason. In either case, responses are not obtained from a
sampled person, and bias is introduced. The problem of
nonresponse is even greater when self-administered
questionnaires are used rather than an interviewer, who can
attempt to reduce the nonresponse rate by means of callbacks. As
noted earlier, a high nonresponse rate, resulting in a biased,
self-selected sample.
3- Selection Bias.
Selection bias occurs when the sampling plan is such that some
members of the target population cannot possibly be selected for
inclusion in the sample.
Together with nonreponse error, selection biases played a role
in pool being so wrong, as voters without telephones or without
a subscription were excluded from possible inclusion in the
sample taken. |
|
2.6 Summary
Because most populations are very large, it is
extremely costly and impractical to investigate each member of
the population to determine the values of the parameters. As a
practical alternative, we take a sample from the population and
use the sample statistics to draw inferences about the
parameters. Care must be taken to ensure that the sampled
population is the same as the target population.
We can choose from among several different sampling plans,
including simple random sampling, stratified random sampling,
and cluster sampling. Whatever sampling plans used, it is
important to realize that both sampling error and nonsampling
error will occur, and to understand what the sources of these
errors are. |
|
|
|
|
|