|
Introduction
When
we are about to describe a set of data, it is a sound advice to
say neither too little nor too much. Thus, depending on the
nature of the data and the purpose we have in mind, statistical
descriptions can be very brief or very elaborate. Sometimes we
present data just as they are and let them speak for themselves;
on other occasions we may just group the data and present their
distribution in tabular or graphical form. Most of the time,
though, we have to describe data in various other ways.
It
is often appropriate to summarize data by means of a few
well-chosen numbers that, in their way, are descriptive of the
entire set. Exactly what sort of numbers we choose depends on
the particular characteristics we want to describe.
In one study we may be interested in a value that somehow
describes the middle or the most typical of a set of data; in
another we may be interested in the value that is exceeded only
by 25% of the data; and in still another we may be interested in
the length of the interval between the smallest and the largest
values among the data. The statistical measures cited in the
first two situations come under the heading of measures of
location and the one cited in the third situation fits the
definition of a measure of variation.
In this chapter, we shall concentrate on measures of location,
and in particular on measures of central location, which in some
way describe the center or the middle of a set of data. Measures
of variation and some other kinds of statistical descriptions
will be discussed in next Chapter. |
|
4.1 Populations and Samples
When
we stated that the choice of a statistical description may
depend on the nature of the data, we were referring among other
things to the following distinction:
If a
set of data consists of all conceivably possible (or
hypothetically possible) observations of a given phenomenon, we
call it a population; if a set of data consists of only a part
of these observations, we call it a sample.
Here, we added the phrase "hypothetically possible" to take care
of such clearly hypothetical situations as where we look at the
outcomes (heads or tails) of 12 flips of a coin as a sample from
the potentially unlimited number of flips of the coin, where we
look at the weights of ten 30-day-old lambs as a sample of the
weights of all (past, present, and future) 30-day-old lambs
raised at a certain farm, or where we look at four determination
of the uranium content of an ore as a sample of the many
determinations that could conceivably be made. In fact, we often
look at the results of an experiment as a sample of what we
might get if, the experiment were repeated over and over again.
Originally, statistics dealt with the description of human
populations, census, counts and the like, but as it grew in
scope, the term "population" took on the much wider connotation
given to it in the preceding distinction between populations and
samples. Whether or not it sounds strange to refer to the
heights of all the trees in a forest or the speeds of all the
cars passing a checkpoint as populations is beside the point-in
statistics, "population" is a technical term with a meaning of
its own.
Although we are free to call any group of items a population,
what we do in practice depends on the context in which the items
are to be viewed. Suppose, for instance, that we are offered a
lot of 400 ceramic tiles, which we may or may not buy depending
on their strength. If we measure the breaking strength of 20 of
these tiles in order to estimate the average breaking strength
of all the tiles, these 20 measurements are a sample from the
population that consists of the breaking strengths of the 400
tiles. In another context, however, if we consider entering into
a long-term contract calling for the delivery of tens of
thousands of such tiles, we would look upon the breaking
strengths of the original 400 tiles only as a sample. Similarly,
the complete figures for a recent year, giving the elapsed times
between the filing and disposition of divorce suits in a County,
can be looked upon as either a population or a sample. If we are
interested only in a County and that particular year, we would
look upon the data as a population; on the other hand, if we
want to generalize about the time that is required for the
disposition of divorce suits in: the entire Country, in some
other County, or in some other year, we would look upon the data
as a sample.
As
we have used it here, the word "sample" has very much the same
meaning as it has in everyday language. A newspaper considers the attitudes of 150 readers toward a
proposed school bond to be a sample of the attitudes of all its
readers toward the bond; and a consumer considers a box of Mrs.
See's candy a sample of the firm's product. Later, we shall
use the word "sample" only when referring to data that can
reasonably serve as the basis for valid generalizations about
the populations from which they came; in this more technical
sense, many sets of data that are popularly called samples are
not samples at all.
In
this chapter and in the next one we shall describe things
statistically without making any generalizations. For future
reference, though, it is important to distinguish even here
between populations and samples. Thus, we shall use different
symbols depending on whether we are describing populations or
samples. |
|
4.2 The Mean
The
most popular measure of central location is what the lay person
calls an "average" and what the statistician calls an arithmetic
mean, or simply a mean.
It is defined as follows:
The
mean of n numbers is their sum divided by n
It
is all right to use the word "average," and on occasion we shall
use it ourselves, but there are other kinds of averages in
statistics and we cannot afford to speak loosely when there is
any risk of ambiguity.
Example (1)
From 1990 through 1994, the combined seizure of drugs the Drug
Enforcement Administration, Custom's Service added up to 1,794,
3,030, 2,551, 3,514, and 2,824 pounds. Find the mean seizure of
drugs for the given five-year period.
Solution:
The
total for the five years is:
1,794 + 3,030 + 2,551 +3,514 + 2,824 = 13,713
Pounds, so that the mean is
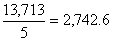 pounds. pounds.
Example (2):
In
the 9th through 97th Congress of Egypt, there were,
respectively, 67, 71, 78, 82, 96, 110, 104, and 92
Representatives at least 60 years old at the beginning of the
first session. Find the mean.
Solution:
The
total of these figures is 67+ 71 + 78 + 82 + 96 + 110 + 104 + 92
= 700. Hence, the mean is
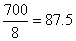 . .
Since we shall have occasion to calculate the means of many
different sets of sample data, it will be convenient to have a
simple formula that is always applicable. This requires that
we represent the figures to be averaged by some general symbol
such as x, y, or z; the number of values in a sample, the sample
size, is usually denoted by the letter n. Choosing the letter x,
we can refer to the n values in a sample as x1, x2,
…, and xn (which read "x sub-one," "x sub-two," ...,
and "x sub-n"), and write
Sample mean = 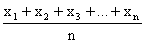
This
formula will take care of any set of sample data, but it can be
made more compact by assigning the sample mean the symbol
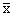 (which
reads “x bar") and using the (which
reads “x bar") and using the
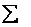 notation.
The symbol notation.
The symbol 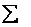 is
capital sigma, the Greek letter for S. In this notation
we let is
capital sigma, the Greek letter for S. In this notation
we let 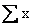 ;
stand for "the sum of the x's" (that is, ;
stand for "the sum of the x's" (that is,
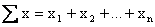 ),
and we can write ),
and we can write
If
we refer to the measurements as y's or z's, we write their mean
as 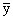 or or
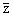 .
In the formula for .
In the formula for 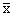 the
term the
term 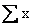 does
not state explicitly which values of x are added; let it
be understood, however, that does
not state explicitly which values of x are added; let it
be understood, however, that
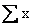 always
refers to the sum of all the x's under consideration in a given
situation. always
refers to the sum of all the x's under consideration in a given
situation.
The
number of values in a population, the population size, is
usually denoted by N.
The
mean of a population of N items is defined in the same way as the mean of a sample.
It
is the sum of the N items,
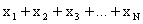 or or
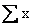 divided
by N. divided
by N.
Assigning the population mean the symbol
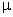 (mu,
the Greek letter for lowercase m) we write (mu,
the Greek letter for lowercase m) we write
With
the reminder that 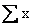 is
now the sum of all N values of x that constitute the
population. is
now the sum of all N values of x that constitute the
population.
Also, to distinguish between descriptions of populations and
descriptions of samples, we not only use different symbols such
as 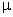 and and
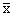 ,
but we refer to a description of a population as a parameter and
a description of a sample as a statistic. Parameters are usually
denoted by Greek letters. ,
but we refer to a description of a population as a parameter and
a description of a sample as a statistic. Parameters are usually
denoted by Greek letters.
To
illustrate the terminology and notation just introduced, suppose
that we are interested in the mean lifetime of a production lot
of N = 40,000 light bulbs. Obviously, we cannot test all of the
light bulbs for there would be none left to use or sell, so we
take a sample, calculate X, and use this quantity as an
estimate of 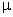 . .
Example (3)
If
n = 5 and the light bulbs in the sample last 967, 949, 952, 940,
and 922 hours, what can we conclude about the mean lifetime of
the 40,000 light bulbs in the production lot?
Solution:
The
mean of this sample is
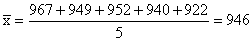 hours hours
If
we can assume that the data constitute a sample in the technical
sense (namely, a set of data from which valid generalizations
can be made), we estimate the mean of all 40,00 light bulbs as
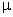 =
946 hours. =
946 hours.
For
nonnegative data, the mean not only describes their middle, but
it also puts some limitation on their size.
If we multiply by n on both sides of the equation
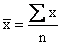 ,
we find that ,
we find that 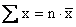 and,
hence, that no part, or subset of the data can exceed and,
hence, that no part, or subset of the data can exceed
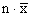 . .
Example (4)
If
the mean salary paid to three NBA players for the 1998-1999
season is $2,450,000, can:
a.
Anyone of them receive an annual salary
of $4,000,000;
b.
Any two of them receive an annual salary
of $4,000,000?
Solution:
The
combined salaries of the three players total 3(2,450,000) =
$7,350,000.
a.
If one of them receives an annual salary
of $4,000,000, this would leave 7,350,000 - 4,000,000 =
$3,350,000 for the other two players, so this could be the case.
b.
For two of them to receive an annual
salary of $4,000,000 would require 2(4,000,000 = $8,000,000,
which exceeds the total paid to the three players. Hence, this
cannot be the case.
Example (5)
If
six high school juniors averaged 57 on the verbal part of the
PSAT/MSQT test, at most how many of them could have scored 72 or
better on the test?
Solution:
Since n = 6 and x = 57, it follows that their combined scores
total 6(57) = 342. Since 342 = 4 x 72 + 54, we find that at most
four of the six students could have scored 72 or more.
The
popularity of the mean as a measure of the "middle" or "center"
of a set of data is not accidental. Anytime we use a single number to describe some aspect of a
set of data, there are certain requirements, or desirable
features, that should be kept in mind. Aside from the fact that
the mean is a simple and familiar measure, the following are
some of it- noteworthy properties:
1-
The
mean can be calculated for any set of numerical data, so it
always exists.
2-
Any
set of numerical data has one and only one mean, so it is always
unique.
3-
The
mean lends itself to further statistical treatment; for
instance, as we shall see, the means of several sets of data can
always be combined into the overall mean of all the data.
4-
The
mean is relatively reliable in the sense that means of repeated
samples drawn from the same population usually do not fluctuate,
or vary, as widely as other statistical measures used to
estimate the mean of a population.
Finally, let us consider another property of the mean that, on
the surface, seems desirable.
5-
The mean takes into account each item in a set of data.
Note, however, that samples may contain very small or very large
values that are so far removed from the main body of the data
that the appropriateness of including them in the sample is
questionable. Such values may be due to chance, they may be due
to gross errors in recording the data, gross errors in
calculations, malfunctioning of equipment, or other identifiable
sources of contamination. In any case, when such values are
averaged in with the other values, they can affect the mean to
such an extent that it is debatable whether it really provides a
useful, or meaningful, description of the "middle" of the data.
Example (6)
The
editor of a book on nutritional values needs a figure for the
calorie count of a slice of a l2-inch pepperoni pizza. Letting a
laboratory with a calorimeter do the job, she gets the following
figures for the pizza from six different fast- food chains: 265,
332, 340, 225, 238, and 346.
a)
Calculate the mean, which the editor
will report in her book.
b)
Suppose that when calculating the mean,
the editor makes the mistake of entering 832 instead of 238 in
her calculator. How much of an error would this make in the
c)
Figure that she reports in her book?
Solution:
a)
The correct mean is:
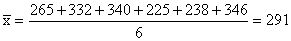
(b)
The correct mean is:
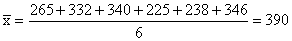
So
that her error would be a disastrous 390-291 = 99.
Example (7)
The
ages of six students who went on a geology field trip are 16,
17, 15, 19, 16, and 17, and the age of the instructor who went
with them is 54. Find the mean age of these seven persons.
Solution:
The
mean is:
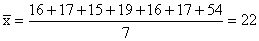
But
any statement to the effect that the average age of the group is
22 could easily be misinterpreted. We might well infer
incorrectly that most of the persons who went on the field trip
are in their low twenties.
To
avoid the possibility of being misled by a mean affected by a
very small value or a very large value, we sometimes find it
preferable to describe the middle or center of a set of data
with a statistical measure other than the mean; perhaps, with
the median, which we shall discuss. |
|
4.3 The Weighted Mean
When
we calculate a mean, we may be making a serious mistake if we
overlook the fact that the quantities we are averaging are not
all of equal importance with reference to the situation being
described. Consider, for example, a cruise line that advertises the
following fares for single-occupancy cabins on an 11-day cruise:
|
Cabin category |
Fare |
|
Ultra deluxe(outside) |
$7,870 |
|
Deluxe (outside) |
$7,080 |
|
Outside |
$5.470 |
|
Outside (shower only) |
$4,250 |
|
Inside (shower only) |
$3.46 |
The
mean of these five fares is
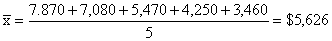
But
we cannot very well say that the average fare for one of these
single occupancy cabins is $5,626. To get that figure, we would
also have to know how many cabins there are in each of the
categories. Referring to the ship's deck plan, where the cabins
are color-coded by category, we find that there are,
respectively, 6, 4, 8, 13, and 22 cabins available in these five
categories. If it can be assumed that these 53 cabins will all
be occupied, the cruise line can expect to receive a total of:
6(7,870)+4(7,080)+8(5,470)+13(4,250)+22(3,460)=250,670
for
the 53 cabins and, hence, on the average
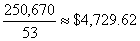 per
cabin. per
cabin.
To
give quantities being averaged their proper degree of
importance, it is necessary to assign them (relative importance)
weights and then calculate a weighted mean.
In general, the weighted mean
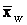 of
a set of numbers x1, x2, x3, …
and xn, whose relative importance is expressed
numerically by a corresponding set of numbers w1, w2,
w3, … and wn is given by: of
a set of numbers x1, x2, x3, …
and xn, whose relative importance is expressed
numerically by a corresponding set of numbers w1, w2,
w3, … and wn is given by:
|
Weighted mean |
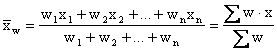 |
Here
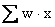 is
the sum of the products obtained by multiplying each x by
the corresponding weight, and is
the sum of the products obtained by multiplying each x by
the corresponding weight, and
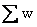 is
simply the sum of the weights. Note that when the weights
are all equal, the formula for the weighted mean reduces to that
for the ordinary (arithmetic) mean. .. is
simply the sum of the weights. Note that when the weights
are all equal, the formula for the weighted mean reduces to that
for the ordinary (arithmetic) mean. ..
Example (8)
The
following Table shows the number of households in the five
Pacific states in 1990, and the corresponding percentage changes
in the number of households 1990-1994:
|
|
Number of households (1,000) |
Percentage change |
|
Washington
Oregon
California
Alaska
Hawaii |
1,872
1,103
10,381
189
356 |
9.1
8.3
4.5
10.3
7.1 |
Calculate the weighted mean of the percentage changes using the
1990 numbers of households as weights.
Solution:
Substituting x1 = 9.1, x2 = 8.3, X3
= 4.5, x4 = 10.3, Xs = 7.1, WI
= 1,872, W2 = 1,103, w3 = 10,381, W4
= 189, and Ws = 356 into the formula for the weighted
mean, we get

Note
that we used the symbol
»
to mean "approximately equal to." We use this symbol only for
steps where numerical rounding occurs.
A
special application of the formula for the weighted mean arises
when we must find the overall mean, or grand mean,
of k sets of data having the means
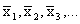 and and
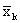 and
consisting of and
consisting of 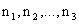 ,
and ,
and 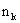 measurements
or observations. The result is given by: measurements
or observations. The result is given by:
|
Grand mean of combined data |
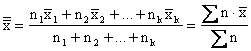 |
Where the weights are the sizes of the samples, the numerator is
the total of all the measurements or observations, and the
denominator is the number of items ~ in the combined samples.
Example (9)
There are three sections of a course in European history, with
19 students in the 1st section meeting MWF at 9 A.M.,
27 in the 2nd section meeting MWF at 11 A.M., and 24
in the 3rd section meeting MWF at 1 P.M. If the
students in the 9 A.M. section averaged 66 in the midterm
examination, those in the 11 A.M. section averaged 71, and those
in the 1 P.M. section averaged 63, what is the mean score for
all three sections combined?
Solution:
Substituting 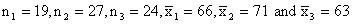 into
the formula for the grand mean of combined data, we get into
the formula for the grand mean of combined data, we get
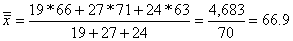
Or
67 rounded to the nearest integer. |
|
4.4 The Median
To avoid the possibility of being misled by one or a few very
small or very large values, we sometimes describe the "middle"
or "center" of a set of data with statistical measures other
than the mean. One of these, the median of n values requires
that we first arrange the data according to size.
Then
it is defined as follows:
The median is the value of the middle item when n is odd, and
the mean of the two middle items when n is even.
In either case, when no two values are alike, the median is
exceeded by as many values as it exceeds. When some of the
values are alike, this may not be the case.
Example (10)
In
five recent weeks, a town reported 36, 29, 42, 25, and 29
burglaries. Find the median number of burglaries for these
weeks.
Solution:
The
median is not 42, the third (or middle) item, because the data
must first be arranged according to size. Thus, we get:
25 29 29 36 42
and it can be seen that the middle one, the median, is 29.
Note
that in this Example there are two 29's among the data and that
we did not refer to either of them as the median - the median
is a number and not necessarily a particular measurement or
observation.
Example (11)
In
some cities, persons cited for minor traffic violations can
attend a class in defensive driving in lieu of paying a fine.
Given that 12 such classes in Phoenix, Arizona, were attended by
37, 32, 28, 40, 35, 38, 40, 24, 30, 37, 32, and 40 persons, find
the median of these data.
Solution:
Ranking these attendance figures according to size, from low to
high, we get
|
|
24 |
28 |
30 |
32 |
32 |
35 |
37 |
37 |
38 |
40 |
40 |
40 |
and
we find that the median is the mean of the two values nearest
the middle namely, 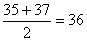
Some
of the values were alike in this example, but not affect the
median, which exceeds six of the values and is exceeded by
equally many. The situation is quite different, however, in the
Example that follows.
Example (12)
On
the seventh hole of a certain golf course, a par four, nine
golfers scored par, birdie (one below par), par, par, bogey (one
above par), eagle (two below par), par, birdie, birdie. Find the
median.
Solution:
Ranking these figures according to size, from low to high, we
get
2 3 3 3 4
4
4 4 5
and
it can be seen that the fifth value, the median, is equal to par
4.
This
time the median exceeds four of the values but is exceeded by
only one, and it may well be misleading to think of the median,
4, as the middle of the nine scores. It is not exceeded by as
many values as it exceeds, but by definition the median is 4.
The
symbol that we use for the median of n sample values x1,
x2, x3, …, and xn (and, hence,
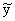 or or
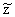 if
we refer to the values of y's or z's) is
m. If a set of data constitutes a population, we
denote its median by if
we refer to the values of y's or z's) is
m. If a set of data constitutes a population, we
denote its median by
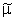 . .
Thus, we have a symbol for the median, but no formula; there is
only a formula for the median position.
Referring again to data arranged according to size, usually ranked
from low to high, we can write
|
Median position |
The median is the value of the
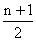 th
item th
item |
Example (13)
Find
the median position for
(a) n = 17; (b) n = 41.
Solution:
With
the data arranged according to size (and counting from either
end)
(a)
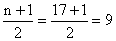 and
the median is the value of the 9th item; and
the median is the value of the 9th item;
(b)
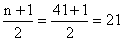 and
the median is the value of the 21st item. and
the median is the value of the 21st item.
Example (14)
Find
the median position for
(a) n = 16;
(b) n = 50.
Solution:
With
the data arranged according to size (and counting from either
end)
(a)
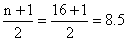 and
the median is the mean of the values of the 8th and 9th
items; and
the median is the mean of the values of the 8th and 9th
items;
(b)
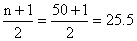 and
the median is the mean of the values of the 25th and
26th items. and
the median is the mean of the values of the 25th and
26th items.
It is important to remember that
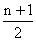 is
the formula for the median position and not a formula for the
median, itself. It is also worth mentioning that determining the
median can usually be simplified, especially for large sets of
data, by first presenting the data in the form of a
stem-and-leaf display. is
the formula for the median position and not a formula for the
median, itself. It is also worth mentioning that determining the
median can usually be simplified, especially for large sets of
data, by first presenting the data in the form of a
stem-and-leaf display.
Example (15)
We
gave data on the number of rooms occupied each day in a resort
hotel during the month of June, and we displayed these data as
follows:
2
3 57
6
4 0023
13
4 5666899
(3)
5 234
14
5 56789
9
6 1224
5
6 9
4
7 23
2
7 8
1
8 1
Use
this double-stem display to find the median of these
room-occupancy data.
Solution:
When
we gave this display in earlier, we did not explain the
significance of the figures in the column to the left of the
stem labels. As can easily be verified, they are simply
the accumulated numbers of leaves counted from either end.
Furthermore, the parentheses around the 3 are meant to tell
us that the median of the data are on that stem (or else are the
mean of two values on that stem).
Since n = 30 for the given table, the median position is
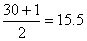 ,
so that the median is the mean of the fifteenth and sixteenth
largest values among the data. Since 2 + 4 + 7 = 13 of the
values are represented by leaves on the first three stems, the
median is the mean of the values represented by the second and
third leaves on the fourth stem. These are 53 and 54, and hence
the median of the room-occupancy data is ,
so that the median is the mean of the fifteenth and sixteenth
largest values among the data. Since 2 + 4 + 7 = 13 of the
values are represented by leaves on the first three stems, the
median is the mean of the values represented by the second and
third leaves on the fourth stem. These are 53 and 54, and hence
the median of the room-occupancy data is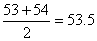 .
Note that this illustrates why we said that it is generally
advisable to arrange the leaves on each stem, so that they are
ranked from low to high. .
Note that this illustrates why we said that it is generally
advisable to arrange the leaves on each stem, so that they are
ranked from low to high.
As a
matter of interest, let us also mention that the mean of the
room-occupancy data is 55.7. It really should not come as a
surprise that the median does not equal the mean-it defines the
middle of a set of data in a different way. The median is
average in the sense that it splits the data into two parts so
that, unless there are duplicates, there are equally many values
above and below the median. The mean, on the other hand, is
average in the sense that if each value is replaced by some
constant k while the total remains unchanged, this number k will
have to be the mean. (This follows directly from the
relationship, 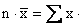 )
In this sense, the mean has also been likened to a center of
gravity. )
In this sense, the mean has also been likened to a center of
gravity.
The
median shares some, but not all, of the properties of the mean.
Like the mean, the median always exists and it is unique
for any set of data. Also like the mean, the median is simple
enough to find once the data have been arranged according to
size, but as we indicated earlier, sorting a set of data
manually can be a surprisingly difficult task.
Unlike the mean, the medians of several sets of data cannot generally be combined
into an overall median of all the data, and in problems of
statistical inference the median is usually less reliable than
the mean. This is meant to say that the medians of repeated
samples from the same population will usually vary more widely
than the corresponding means. On the other hand, sometimes the
median may be preferable to the mean because it is not so
easily, or not at all, affected by extreme (very small or very
large) values.
For instance, we showed that incorrectly entering 832 instead of
238 into a calculator caused an error of 99 in the mean. As the
reader will be asked to verify, the corresponding error in the
median would have been only 37.5.
Finally, also unlike the mean, the median can be used
to define the middle of a number of objects, properties, or
qualities that can be ranked, namely, when we deal with ordinal
data. For instance, we might rank a number of tasks
according to their difficulty and then describe the middle (or
median) one as being of "average difficulty." Also, we might
rank samples of chocolate fudge according to their consistency
and then describe the middle (or median) one as having "average
consistency."
Besides the median and the mean there are several other measures
of central location; for example, the midrange described
and the mid quartile. Each describes the "middle" or
"center" of a set of data in its own way, and it should not come
as a surprise that their values may well all be different. Then
there is also the mode. |
|
4.5 Other Fractiles
The
median is but one of many fractiles that divide data into two
or more parts, as nearly equal as they can be made. Among them
we also find quartiles, deciles, and percentiles, which are
intended to divide data into four, ten, and a hundred parts.
Until recently, fractiles were determined mainly for
distributions of large sets of data.
In
this section, we shall concern ourselves mainly with a problem
that has arisen in exploratory data analysis - in the
preliminary analysis of relatively small sets of data. It is the
problem of dividing such data into four nearly equal parts,
where we say "nearly equal" because there is no way in which we
can divide a set of data into four equal parts for, say, n = 27
or n = 33. Statistical measures designed for this purpose have
traditionally been referred to as the three quartiles, Q1,
Q2, and Q3, and there is no argument about
Q2, which is simply the median. On the other hand,
there is some disagreement about the definition of Q1,
and Q3.
As
we shall define them, the quartiles divide a set of data into
four parts such that there are as many values less than Q1
as there are between Q1 and Q2 between Q2
and Q3, and greater than Q3. Assuming that
no two values are alike, this is accomplished by letting
Q1
be the median of all the values less than the median of the
whole set of data, and Q3 be the median of all the
values greater than the median of the whole set of data.
Example (16)
Following are the high-temperature readings in twelve European
capitals on a recent day in the month of June: 90, 75, 86, 77,
85,72,78,79,94,82,74, and 93. Find Q1, Q2
(the median), and Q3.
Solution:
For
n = 12 the median position is
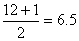 and,
after arranging the data according to size, we find that the
sixth and seventh values among and,
after arranging the data according to size, we find that the
sixth and seventh values among
|
|
72 |
74 |
75 |
77 |
78 |
79 |
82 |
85 |
86 |
90 |
93 |
94 |
are
79 and 82. Hence the median is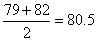 .
For the six values below 80.5 the median position is .
For the six values below 80.5 the median position is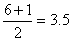 ,
and since the third and fourth values are 75 and 77, ,
and since the third and fourth values are 75 and 77,
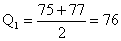 Counting
from the other end, the third and fourth values are 90 and 86,
and Counting
from the other end, the third and fourth values are 90 and 86,
and 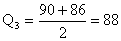 .
As can be seen from the data and also from figure 4.1, there are
three values below 76, three values between 76 and 80.5, three
values between 80.5 and 88, and three values above 88. .
As can be seen from the data and also from figure 4.1, there are
three values below 76, three values between 76 and 80.5, three
values between 80.5 and 88, and three values above 88.
Figure 4.1:
Three quartiles of Example 3.16
Everything worked nicely in this example, but n = 12 happened to
be a multiple of 4, which raises the question whether our
definition of Q1 and Q3 will work also
when this is not the case.
Example (17)
Suppose that the city where the high temperature was 77 failed
to report, so that we are left with the following 11 numbers
arranged according to size:
|
|
72 |
74 |
75 |
78 |
79 |
82 |
85 |
86 |
90 |
93 |
94 |
Solution:
For
n = 11 the median position is
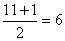 and,
referring to the preceding data, which are already arranged
according to size, we find that the median is 82. For the five
values below 82 the median position is and,
referring to the preceding data, which are already arranged
according to size, we find that the median is 82. For the five
values below 82 the median position is
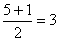 ,
and Q1, the third value, equals 75. Counting from the
other end, Q3, the third value, equals 90. As can be
seen from the data and also from figure 4.2, there are two
values below 75, two values between 75 and 82, two values
between 82 and 90, and two values above 90. Again, this
satisfies the requirement for the three quartiles, Q1,
Q2, and Q3. ,
and Q1, the third value, equals 75. Counting from the
other end, Q3, the third value, equals 90. As can be
seen from the data and also from figure 4.2, there are two
values below 75, two values between 75 and 82, two values
between 82 and 90, and two values above 90. Again, this
satisfies the requirement for the three quartiles, Q1,
Q2, and Q3.
Figure 4.2:
Three quartiles of Example 3.17
If
some of the values are alike, we modify the definitions of Q1
and Q3 by replacing "less than the median" by "to the
left of the median position" and "greater than the median" by
"to the right of the median position". For instance, for Example (12), we already showed that the
median, the fifth value, equals 4. Now, the median of the four
values to the left of the median position, Q1, equals
3, and the median of the four values to the right of the median
position, Q3, equals 4.
Quartiles are not meant to be descriptive of the "middle" or
"center" of a set of data, and we have given them here mainly
because, like the median, they are fractiles and they are
determined in more or less the same way. The midquartile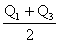 has
been used on occasion as another measure of central location. has
been used on occasion as another measure of central location.
The
information provided by the median, the quartiles Q1
and Q3, and the smallest and largest values is
sometimes presented in the form of a box plot.
Originally referred to somewhat whimsically as a
box-and-whisker plot, such a display consists of a
rectangle that extends from Q1 to Q3,
lines drawn from the smallest value to Q1 and from Q3
to the largest value, and a line at the median that divides the
rectangle into two parts. In practice, box plots are sometimes
embellished with other features, but the simple form shown here
is adequate for most purposes.
Example (18)
In
Example 15 we used the following double-stem display to show
that the median of the room occupancy data, originally given
before is 53.5:
2 3 57
6 4 0023
13 4 5666899
(3) 5 234
14 5 56789
9 6 1224
5 6 9
4 7 23
2 7 8
1 8 1
(a)
Find the smallest and largest values.
(b)
Find Q1 and Q3.
(c)
Draw a box plot.
Solution:
a)
As can be seen by inspection the
smallest value is 35 and the largest value is 81.
b)
For n = 30 the median position is
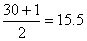 and,
hence, for the 15 values below 53.5 the median position is and,
hence, for the 15 values below 53.5 the median position is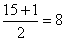 .
It follows that Q1 the eighth value, is 46.
Similarly, Q3, the eighth value from the other end,
is 62. .
It follows that Q1 the eighth value, is 46.
Similarly, Q3, the eighth value from the other end,
is 62.
c)
Combining all this information, we
obtain the box plot shown in Figure 4.3.
30 40 50
60 70 80
Smallest value Q1 Median Q2
largest
value
Figure 4.3: Box plot of room occupancy data
Box
plots can also be constructed with appropriate computer software
or a graphing calculator. Using same data as in Example 18, we
reproduced the one shown in Figure 4.4 from the display screen
of a TI-83 graphing calculator.
Figure 4.4: Box plot of room occupancy data (TI-83 graphing) |
|
4.6 The Mode
Another measure that is sometimes used to describe the middle or
center of a set of data is the mode, which is defined simply as
the value that occurs with the highest frequency and more than
once. Its two main advantages are that it requires
no calculations, only counting, and it can be determined for
qualitative, or nominal, data.
Example (19)
The
20 meetings of a square dance club were attended by 22, 24, 23,
24, 27, 25, 20, 24, 26, 28, 26, 23, 21, 24, 24, 25, 23, 28, 26,
and 25 of its members. Find the mode.
Solution:
Among these numbers, 20, 21, 22, and 27 each occurs once, 28
occurs twice, 23, -25, and 26 each occurs three times; and 24
occurs 5 times. Thus, the modal attendance is 24.
Example (20)
In
Example 12, we gave the scores of nine golfers on a par-four
hole as 2, 3, 3, 3, 4, 4, 4, 4, and 5. Find the mode.
Solution:
Since these data are already arranged according to size, it can
easily be seen that 4, which occurs four times, is the modal
score.
As
we have seen in this chapter, there are various measures of
central location that describe the middle of a set of data. What
particular "average" should be used in any given situation can
depend on many different things and the choice may be difficult
to make. Since the selection of statistical descriptions often
contains an element of arbitrariness, some persons believe that
the magic of statistics can be used to prove nearly anything.
Indeed, a famous nineteenth-century British statesman is often
quoted as saying that there are three kinds of lies: lies,
damned lies, and statistics. |
|
4.7 The Description of Grouped Data
In
the past, considerable attention was paid to the description of
grouped data, because it usually simplified matters to group
large sets of data before calculating various statistical
measures. This is no longer the case, since the necessary
calculations can now be made in a matter of seconds with the use
of computers or even hand-held calculators. Nevertheless, we
shall devote this section to the description of grouped data,
since many kinds of data (for example, those reported in
government publications) are available only in the form
frequency distributions.
As
we have already seen, the grouping of data entails some loss of
information. Each item loses its identity, so to speak; we know
only how many values there are in each class or in each
category. This means that we shall have to be satisfied with
approximations. Sometimes we treat our data as if all the
values falling into a class were equal to the corresponding
class mark, and we shall do so to define the mean of a frequency
distribution. Sometimes we treat our data as if all the values
falling into a class are spread evenly throughout the
corresponding class interval, and we shall do so to define the
median of a frequency distribution. In either case, we get good
approximations since the resulting errors will tend to average
out.
To
give a general formula for the mean of a distribution with k
classes, let us denote the successive class marks by x1,
x2 ..., and xk, and the corresponding
class frequencies by f1, f2, …, and fk.
Then, the sum of all the measurements is approximated by:
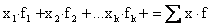 and
the mean of the distribution is given by and
the mean of the distribution is given by
|
Mean of grouped data |
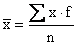 |
Here
n is the size of the sample, f1 + f2 +
...+ f3, and to write a corresponding formula for the
mean of a population we substitute
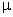 for for
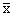 and
N for n. and
N for n.
Example (21)
Find
the mean for the distribution of the waiting times between
eruptions of Old Faithful Geyser that was obtained in Example
before.
Solution:
To
get 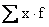 ,
we perform the calculations shown in the following table, where
the first column contains the class marks, the second column
consists of the class frequencies shown on page 24, and the
third column contains the products x. f: ,
we perform the calculations shown in the following table, where
the first column contains the class marks, the second column
consists of the class frequencies shown on page 24, and the
third column contains the products x. f:
|
Class Mark
x |
Frequency
f |
 |
|
34.5
44.5
54.5
64.5
74.5
84.5
94.5
104.5
114.5 |
2
2
4
19
24
39
15
3
2 |
69.0
89.0
218.0
1,225.5
1,788.0
3,295.5
1,417.5
313.5
229.0 |
|
|
110 |
8,645.0 |
Then, substitution into the formula yields
 rounded
to two decimals. rounded
to two decimals.
To
check on the grouping error, namely, the error introduced by
replacing each value within a class by the corresponding class
mark, we can calculate
 for
the original data, or use the same computer software. Having already entered the data, we simply change
the command to MEAN C1 and we get 78.273, or 78.27 rounded to
two decimals. Thus, the grouping error is only 78.59 -78.27 =
0.32, which is fairly small. for
the original data, or use the same computer software. Having already entered the data, we simply change
the command to MEAN C1 and we get 78.273, or 78.27 rounded to
two decimals. Thus, the grouping error is only 78.59 -78.27 =
0.32, which is fairly small.
When
dealing with grouped data, we can determine most other
statistical measures besides the mean, but we may have to make
different assumptions and / or modify the definitions.
For instance, for the median of a distribution we use the
assumption (namely, the assumption that the values within a
class are spread evenly throughout the corresponding class
interval). Thus, with reference to a histogram
The
median of a distribution is such that the total area of the
rectangles to its left equals the total area of the rectangles
to its right.
To
find the dividing line between the two halves of a histogram
(each of which represents
 of
the items grouped), we must count of
the items grouped), we must count
 of
the items starting at either end of the distribution. How this
is done is illustrated by the following Example and Figure 4.5. of
the items starting at either end of the distribution. How this
is done is illustrated by the following Example and Figure 4.5.

Figure 4.5: Median of distribution of eruptions of old
faithful
Example (22)
Find
the median of the distribution of the waiting times between
eruptions of Old Faithful.
Solution:
Since ,
we must count 55 of the items starting at either end. Starting
at the bottom of the distribution (that is, beginning with the
smallest values), we find that 2 + 2 + 4 + 19 + 24 = 51 of the
values fall into the first five classes. Therefore, we must
count 55 -51 = 4 more values from among the values in the sixth
class. Based on the assumption that the 39 values in the sixth
class are spread evenly throughout that class, we accomplish
this by adding ,
we must count 55 of the items starting at either end. Starting
at the bottom of the distribution (that is, beginning with the
smallest values), we find that 2 + 2 + 4 + 19 + 24 = 51 of the
values fall into the first five classes. Therefore, we must
count 55 -51 = 4 more values from among the values in the sixth
class. Based on the assumption that the 39 values in the sixth
class are spread evenly throughout that class, we accomplish
this by adding  of
the class interval of 10 to 79.5, which is its lower class
boundary. This yields: of
the class interval of 10 to 79.5, which is its lower class
boundary. This yields:

Rounded to two decimals.
In
general, if L is the lower boundary of the class into which
the median must fall, f is its frequency, c is its class
interval, and j is the number of items we still lack when we
reach L, then the median of the distribution is given by
|
Median of grouped data |
 |
If
we prefer, we can find the median of a distribution by starting
to count at the other end (beginning with the largest values)
and subtracting an appropriate fraction of the class interval
from the upper boundary of the class into which the median must
fall.
Example (23)
Use
this alternative approach to find the median of the waiting
times between eruptions of Old Faithful.
Solution:
Since 2 + 3 + 15 = 20 of the values fall above 89.5, we need 50
– 20 = 35 of the 39 values in the next class to reach the
median. Thus, we write
 and
the result is, of course, the same. and
the result is, of course, the same.
Note
that the median of a distribution can be found regardless of
whether the class intervals are all equal. In fact, it can be
found even when either or both classes at the top and at the
bottom of a distribution are open, so long as the median does
not belong to either class.
The
method by which we found the median of a distribution can be
also used to determine other fractiles. For instance Q1 and Q3 are defined for
grouped data so that 25% of the total area of the rectangles of
the histogram lies to the left of Q1 and 25% lies to
the right of Q3. Similarly, the nine deciles (which
are intended to divide a set of data into ten equal parts) are
defined for grouped data so that 10 percent of the total area of
the rectangles of the histogram lies to the left of D1,
10 percent lies between D1 and D2, …, and
10 percent lies to the right of D9. And finally, the
ninety-nine percentiles (which are intended to divide a set of
data into a hundred equal parts) are defined for grouped data so
that 1 percent of the total area of the rectangles of the
histogram lies to the left of P1, 1 percent lies
between P1 and P2, … and 1 percent lies to
the right of P99. Note that Ds and P50
are equal to the median and that P25 equals Q1
and P75 equals Q3.
Example (24)
Find
Q1 and Q3 for the distribution of the
waiting times between eruptions of Old Faithful.
Solution:
To
find Q1 we must count
 of
the items starting at the bottom of the distribution. Since
there are 2+2+4+19 = 27 values in the first four classes, we
must count 27.5 – 27 = 0.5 of the 24 values in the fifth class
to reach Q1. This yields: of
the items starting at the bottom of the distribution. Since
there are 2+2+4+19 = 27 values in the first four classes, we
must count 27.5 – 27 = 0.5 of the 24 values in the fifth class
to reach Q1. This yields:

Since 2+3+15=20 of the values fall into the last three classes,
we must count 27.5 - 20 = 7.5 of the 39 values in the next class
to reach Q3. Thus, we write

Example (25)
Find
D2 and P8 for the distribution of the
waiting times between eruptions of Old Faithful.
Solution:
To
find D2 we must count
 of
the items starting at the bottom of the distribution. Since
there are 2+2+4=8 values in the first three classes, we must
count 22-8= 14 of the 19 values of the fourth class to reach D2.
This yields of
the items starting at the bottom of the distribution. Since
there are 2+2+4=8 values in the first three classes, we must
count 22-8= 14 of the 19 values of the fourth class to reach D2.
This yields

Since 2+3+15=20 of the values fall into the last three classes,
we must count 22-20 = 2 of the 39 values in the next class to
reach P8. Thus, we write

Note
that when we determine a fractile of a distribution, the number
of items we have to count and the quantity j in the formula on
page 73 need not be a whole number. |
|
|
|
|