|
6.3 Least Squares Method
We
estimate the parameters
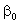 and and
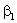 in
a way similar to the methods used to estimate all the other
parameters discussed in this notes. We draw a random sample from
the populations of interest and calculate the sample statistics
we need. Because in
a way similar to the methods used to estimate all the other
parameters discussed in this notes. We draw a random sample from
the populations of interest and calculate the sample statistics
we need. Because 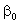 and and
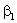 represent
the coefficients of a straight line, their estimators are based
on drawing a straight line through the sample data. To see
how this is done, consider the following simple example. represent
the coefficients of a straight line, their estimators are based
on drawing a straight line through the sample data. To see
how this is done, consider the following simple example.
Example (4)
Given the following six observations of variables x and
y,-determine the straight line that fits these data.
|
x |
2 |
4 |
8 |
10 |
13 |
16 |
|
y |
2 |
7 |
25 |
26 |
38 |
50 |
Solution:
As a
first step we graph the data, as shown in the figure. Recall
that this graph is called a scatter diagram. The scatter diagram
usually reveals whether or not a straight line model fits the
data reasonably well. Evidently, in this case a linear model is
justified. Our task is to draw the straight line that provides
the best possible fit.

Scatter Diagram for Example
We
can define what we mean by best in various ways. For example, we
can draw the line that minimizes the sum of the differences
between the line and the points. Because some of the differences
will be positive (points above the line), and others will be
negative (points below the line), a canceling effect might
produce a straight line that does not fit the data at all. To
eliminate the positive and negative differences, we will draw
the line that minimizes the sum of squared differences. That is,
we want to determine the line that minimizes.
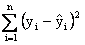
Where yi represents the observed value of y and
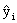 represents
the value of y calculated from the equation of the line. That
is, represents
the value of y calculated from the equation of the line. That
is,
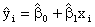
The
technique that produces this line is called the least squares
method.
The line itself is called the least squares line, or
the regression line. The "hats" on the coefficients
remind us that they are estimators of the parameters
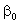 and and
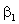 . .
By
using calculus, we can produce formulas for
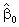 and and
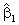 .Although
we are sure that you are keenly interested in the calculus
derivation of the formulas, we will not provide that, because we
promised to keep the mathematics to a minimum. Instead, we offer
the following, which were derived by calculus. .Although
we are sure that you are keenly interested in the calculus
derivation of the formulas, we will not provide that, because we
promised to keep the mathematics to a minimum. Instead, we offer
the following, which were derived by calculus.
Calculation of 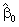 and and
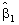 . .
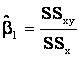
where
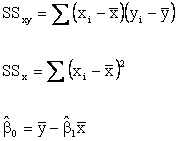
and
where
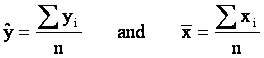
The
formula for SSx should look familiar; it is the
numerator in the calculation of sample variance s2.
We introduced the SS notation; it stands for sum of squares.
The statistic SSx is the sum of squared differences
between the observations of x and their mean. Strictly speaking,
SSxy is not a sum of squares.
The
formula for SSxy may be familiar; it is the
numerator in the calculation for covariance and the coefficient
of correlation.
Calculating the statistics manually in any realistic Example is
extremely time consuming. Naturally, we recommend the use of
statistical software to produce the statistics we need. However,
it may be worthwhile to manually perform the calculations for
several small-sample problems. Such efforts may provide you with
insights into the working of regression analysis. To that end we
provide shortcut formulas for the various statistics that are
computed in this chapter.
Shortcut Formulas for SSx and SSxy
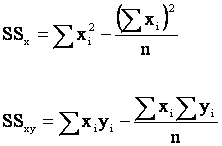
As
you can see, to estimate the regression coefficients by hand,
we need to determine the following summations.
Sum
of x: 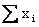
Sum
of y: 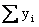
Sum
of x-squared: 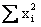
Sum
of x times y: 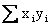
Returning to our Example we find
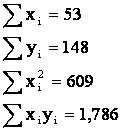
Using these summations in our shortcut formulas, we find
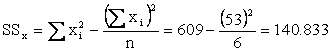
and
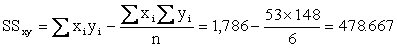
Finally, we calculate
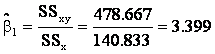
and
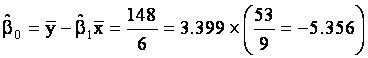
Thus, the least squares line is
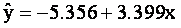
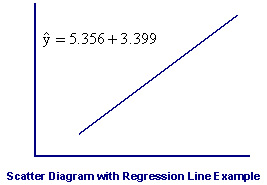
The
next figure describes the regression line. As you can see, the
line fits the data quite well. We can measure how well by
computing the value of the minimized sum of squared differences.
The differences between the points and the line are called
residuals, denoted ri . That is,
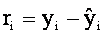
The
residuals are the observed values of the error variable.
Consequently, the minimized sum of squared
differences is called the sum of squares for error denoted
SSE.
Sum
of Squares for Error
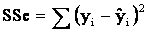
The
calculation of SSE 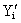 this
Example is shown in the next figure. Notice that we compute
Yi by substituting Xi into the formula for the regression line.
The residuals are the differences between the observed values this
Example is shown in the next figure. Notice that we compute
Yi by substituting Xi into the formula for the regression line.
The residuals are the differences between the observed values
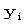 and
the computed values and
the computed values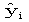 .
The following Table describes the calculation of SSE. .
The following Table describes the calculation of SSE.
|
|
|
|
|
RESIDUAL |
RESIDUAL SQUARED |
|
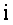 |
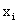 |
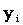 |
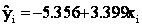 |
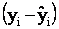 |
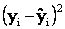 |
|
1
2
3
4
5
6 |
2
4
8
10
13
16 |
2
7
25
26
38
50 |
1.442
8.240
21.836
28.634
38.831
49.028 |
0.558
-1.240
3.164
-2.634
-0.831
0.972 |
0.3114
1.5376
10.0109
6.9380
0.6906
0.9448 |
|
|
|
|
|
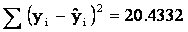 |
Thus, SSE = 20.4332. No other straight line will produce a sum
of squared errors as small as 20.4332. In that sense, the
regression line fits the data best. The sum of squares for error
is an important statistic because it is the basis for other
statistics that assess how well the linear model fits the data.
Example (5)
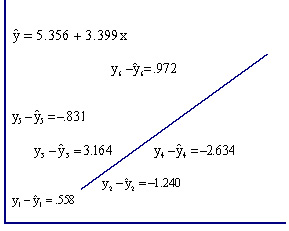
We
now apply the technique to a more practical problem.
Example (6)
Car
dealers across North America use the "Red Book" to help them
determine the value of used cars that their customers trade in
when purchasing new cars. The book, which is published monthly,
lists the trade-in values for all basic models of cars. It
provides alternative values of each car model according to its
condition and optional features. The values are determined on
the basis of the average paid at recent used-car auctions.
(These auctions are the source of supply for many used-car
dealers.) However, the Red Book does not indicate the value
determined by the odometer reading, despite the fact that a
critical factor for used – car buyers is how far the car has
been driven. To examine this issue, a used-car dealer randomly
selected 100 three year of Ford Taurusses that were sold at
auction during the past month. Each car was in top condition and
equipped with automatic transmission, AM/FM cassette tape
player, and air conditioning. The dealer recorded the price and
the number of miles on the odometer. These data are summarized
below. The dealer wants to find the regression line.
Solution:
Notice that the problem objective is to analyze the relationship
between two quantitative variables. Because we want to know how
the odometer reading affects selling price, we identify the
former as the independent variable, which we used, and
the latter as the dependent variable, which we label y.
Solution by Hand:
To
determine the coefficient estimates, we must compute SSx
and SSxy. They are
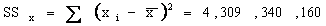
and
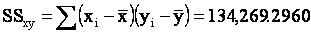
Using the sums of squares, we find the slope coefficient.
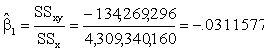
To
determine the intercept, we need to find x and y.
They are
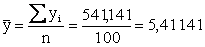
and
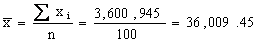
Thus,
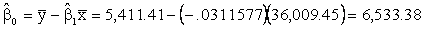
The
sample regression line is
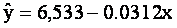
Interpreting The
Coefficient
The
coefficient 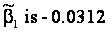 which
means that for each additional mile on the odometer, the price
decreases by an average of $0.0312 (3.12 cents). which
means that for each additional mile on the odometer, the price
decreases by an average of $0.0312 (3.12 cents).
The
intercept is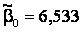 .
Technically, the intercept is the point at which the
regression line and the y-axis intersect. This means that
when x = 0 (i.e., the car was not driven at all) the selling
price is $6,533. We might be tempted to interpret this number as
the price of cars that have not been driven. However, in this
case, the intercept is probably meaningless. Because our sample
did not include any cars with zero miles on the odometer we have
no basis for interpreting .
Technically, the intercept is the point at which the
regression line and the y-axis intersect. This means that
when x = 0 (i.e., the car was not driven at all) the selling
price is $6,533. We might be tempted to interpret this number as
the price of cars that have not been driven. However, in this
case, the intercept is probably meaningless. Because our sample
did not include any cars with zero miles on the odometer we have
no basis for interpreting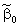 .
As a general rule, we cannot determine the value of y for a
value of x that is far outside the range of the sample values of
x. In this example, the smallest and largest values of x are
19,057 and 49,223, respectively. Because x = 0 is not in this
interval we cannot safely interpret the value of 11 when
x = o. .
As a general rule, we cannot determine the value of y for a
value of x that is far outside the range of the sample values of
x. In this example, the smallest and largest values of x are
19,057 and 49,223, respectively. Because x = 0 is not in this
interval we cannot safely interpret the value of 11 when
x = o. |