7.1 Chi-Squared Test of a
Contingency Table
The
chi-squared test is used to determine if there is enough
evidence to infer that two are related and to infer that
differences exist among two qualitative variables. Completing
both objectives entails to two different criteria.
The following is an Example to see how this is done.
Example (1)
One
of the issues that came up in a recent national election in many
future elections) is how to deal with a sluggish should
governments cut spending, raise taxes, inflate the more money),
or do none of the above and let the deficit rise politicians
need to know which parts of the electorate suppose that a random
sample of 1,000 people was asked which and their political
affiliations. The possible responses to the affiliation were
Democrat, Republican, and Independent. The responses were
summarized in cross-classification table, shown below. Do this
conclude that political affiliation affects support for the
ecology.
|
|
Political Aff. |
|
Economic Opinions |
Democrat |
Republican |
|
Cut spending
Raise taxes
Inflate the economy
Let deficit increase |
101
38
131
61 |
282
67
88
90 |
Solution:
One
way to solve the problem is to consider the contingency table.
The variables are economic affiliation. Both are qualitative.
The values of economic "raise taxes," "inflate the economy," and
"let deficit increase political affiliation are "Democrat,"
"Republican" and "Independent" objective is to analyze the
relationship between the two variables. Specifically, we want to
know whether one variable affects the other.
Another way of addressing the problem is to determine whether
differences exist among Democrats, Republicans, and
Independents. In other words, we treat each political group as a
separate population. Each population has four possible values,
represented by the four economic options. (We can also answer the question by treating the economic
options as populations and the political affiliations as the
values of the random variable.) Here the problem objective is to
compare three populations.
As
you will shortly discover, both objectives lead to the same
test. Consequently, we can address both objectives at the same
time.
The
null hypothesis will specify that there is no relationship
between the two variables. We state this in the following way.
Ho:
The two variables are independent.
The
alternative hypothesis specifies that one variable affects the
other, which is expressed as
HA:
The two variables are dependent.
If
the null hypothesis is true, political affiliation and economic
option are independent of one another.
This means that whether someone is a Democrat, Republican, or
Independent does not affect his economic choice. Consequently,
there is no difference among Democrats, Republicans, and
Independents in their support for the four economic options. If
the alternative hypothesis is true, political affiliation does
affect which economic option is preferred. Thus, there are
differences d is likely to among the three political groups.
The
test statistic is
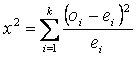
Where k is the number of cells in the contingency table. The null hypothesis for the chi-squared test
of a contingency table only states that the two variables are
independent. However, we need the probabilities in order to
compute the expected values (ej), which in turn
permits us to calculate the value of the test statistic. (The
entries in the contingency table are the observed values, oi.
The question immediately arises: from where do we get the
probabilities? The answer is that they will come from the data
after we assume that the null hypothesis is true.
If
we consider each political affiliation to be a separate
population, each column of the contingency table represents an
experiment with four cells. If the null hypothesis is true, the
three experiments should produce similar proportions in each
cell. We can estimate the cell probabilities by calculating the
total in each row and dividing by the sample size. Thus,
P(cut spending) 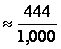
P(raise taxes) 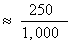
P(let deficit increase)
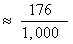
We
can calculate the expected values for each cell in the three by
multiplying these probabilities by the total number of political
group. By adding down each column,
we find that there are residents who identified themselves as
Democrats (331), 527 as Republicans and 142 as independents.
Expected Values of the Economic Options of Democrats
|
EONOMIC OPTION
Cut spending
Raise Taxes
Inflate economy
Let deficit increase |
EXPECTED VALUE
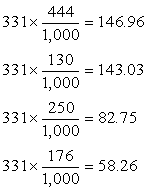 |
|
Expected Values of the Economic Options
of Republicans
|
|
EONOMIC OPTION
Cut spending
Raise Taxes
Inflate economy
Let deficit increase |
EXPECTED VALUE
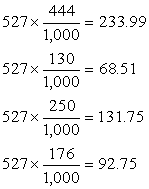 |
|
Expected Values of the Economic Options
of Independents
|
|
EONOMIC OPTION
Cut spending
Raise taxes
Inflate economy
Let deficit increase |
EXPECTED VALUE
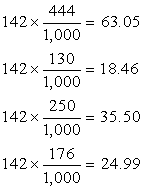 |
Notice
that the expected values are computed by multiplying the column
total by the row total and dividing by the sample size. |