|
Introduction
Price and quality indexes are summary measures of relative price
and quality changes over time in a set of items.
For example, the consumer price index summarizes relative price
changes in goods and services purchased by urban households; the
producer price indexes measure changes in prices received in
primary markets by producers of commodities in all stages of
processing; and the index of industrial production measures
relative changes in output in manufacturing, mining and
utilities.
Price and quality indexes not only serve as summary measures of
price and quality changes but also are employed in many
analyses. Regression models, for instance, frequently contain price
or quality indexes as independent variables. Another use of
price indexes is to adjust time series expressed in monetary
units, such as annual sales revenues during the past 20 years,
so that changes in the series other than price changes can be
studied.
In
this chapter, we discuss price and quality indexes in their
several roles. First we take up the construction of price
indexes various uses of them. Then we discuss quantity indexes.
Percent Relatives and Link Relatives
We
begin with the measurement of price changes for a single item,
such as a gallon of 89 octane unleaded gasoline or a
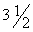 inch
high-density computer disk. inch
high-density computer disk.
Present Relatives
Percent relatives are useful for studying the pattern of
relatives changes in the price of an item over time.
Example: Chemical Compound
The
average price of a chemical compound for each year in the period
1988 – 1991 is shown in the Table below. The corresponding
percent relatives, calculated on the base period 1988 are shown
in column 2. For instance, the percent relative for 1989 is 100
(22/20) = 110. This relative tells us that the price of the
compound in 1989 was 110 percent as great as in 1988.
Calculation of percent relative and link
relatives series – chemical compound example
|
Year |
(1) |
(2) |
(3) |
(4) |
|
Average Price (dollars) |
Percent Relatives |
Link Relative |
|
1988=100 |
1991=100 |
|
1988
1989
1990
1991 |
20
22
36
50 |
100
110
180
250 |
40
44
72
100 |
-
110
164
139 |
The
base period for a percent relatives series is usually identified
for reporting purposes in the manner shown in the above Table;
for example, 1988 = 100. The base period may be any period that
facilitates the comparisons of interest. For instance, the
choice of 1988 in the chemical compound Example facilitates the
study of the price increases during a period when demand was
increasing rapidly because of a new industrial use for the
compound.
Interpretation of
Percent Relatives
Percent relatives must be interpreted with care. We discuss
briefly three important considerations.
1.
The absolute magnitudes of percent relatives are
affected by the choice of the base period, but their
proportional magnitudes are not affected by this choice. We illustrate this for the chemical compound
Example by presenting in column 3 of the above Table the percent
relatives calculated on the base period 1991. The percent
relative for 1988 now is 100(20/50 = 40, not 100 as for the 1988
base period series. However, the proportional magnitudes of the
percent relatives in columns 2 and 3 are the same. For instance,
the percent relatives for 1989 and 1988, with base period 1988,
have the ratio 110/100 = 1.1. For the percent relatives with the
1991 base period, this ratio is the same; that is, 44/40 = 1.1.
Similarly for both series of percent relatives, the ratio of the
1990 price relative to the 1989 price relative is 1.64.
2.
A comparison of percent relatives for two
different price series indicates nothing about the actual prices
unless we know the actual magnitudes in the base period.
For
example, information that the percent relatives for large
"grade-A" eggs last month were 120 for Montreal and 123 for
Toronto tells us nothing about how the egg prices in the two
cities compared last month unless we know the prices in the base
period.
3.
In analyzing percent relatives, we distinguish
between percent points of change and percent change.
To illustrate the difference, refer to the percent relatives
with base period 1988 in column 2 of the Table for the chemical
compound example. Between 1990 and 1991, the percent points of
change were 250 - 180 = 70. On the other hand, the percent
change was 100[(250-180)/180] = 100(70/180) = 38.9. Thus, a
percent point of change refers to the absolute change in the
percent relatives and is dependent on the choice of the base
period. Percent change, in contrast, refers to the relative
change in percent relative and, as we noted previously, is not
affected by the choice of the base period.
Link
Relatives
Link
relatives are useful in studying relative period-to-period
changes instead of change from a fixed base period. For instance, link relatives enable us to study whether or not the
price of an item is increasing at a constant rate, an increasing
rate, or a decreasing rate.
A
link relative series express the value of the series in each
period as percent of the value in the immediately preceding
period.
Example
The
link relatives for the chemical compound Example are given in
column 4 in the same Table of the above Example. For instance, the link relative for 1989 is 100(22/20) = 110. This
tells us that the price in 1989 was 110 percent as great as in
1988. The link relative for 1990 is 100(36/22) = 164, indicating
that the price in 1990 was 164 percent as great as in 1989. Note
that the percent increase from 1990 to 1991 was smaller than
that from 1989 to 1990 (column 4), even though the amount of
price increase ($14) did not decline (column 1).
Comment
We
have illustrated percent relatives and link relatives for price
series, but these relatives can be utilized for any time series
(for example, annual sales or monthly production). |
|
8.1 Price
Index by Method of Weighted Aggregates
Price indexes are summary measures that combine the price
changes for a group of items, using weights to give each item
its appropriate importance. The consumer price index is such an
index measuring the combined effect of price changes in many
goods and services purchased by urban households. Two basic
methods are widely used for calculating price indexes:
the method of weighted aggregates and the method of weighted
average of relatives. We shall explain each in turn,
using the following illustration.
Example: School Maintenance Supplies
Officials of a large school district needed to develop a price
index for maintenance supplies for the school buildings in the
district. In compiling this index, the officials could not
include all supply items in the index because the number of
supply items used is very large. Instead, a sample of supply
items was selected to represent all items used. The selected
items are shown in Tabulated below, column 1. Also shown in this
table, in columns 3, 4, and 5, are the unit prices of these
items for 1988, 1989 and 1990, respectively. Finally, column 2
of the Table presents typical quantities consumed annually for
each of the selected supply items.
Method of Weighted
Aggregates
The
method of weighted aggregates for compiling a price index simply
compares the cost of the typical quantities consumed at the
prices of a given period with the corresponding cost in the base
period. We shall first explain the notation and terminology used we
illustrate the method of calculation by an example.
Calculation of price index series by method
of weighted aggregates-school maintenances supplies example
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
|
Schedule of Items |
Quantity
 |
Unit Price |
P10Q12
(3) x (2) |
P11Q12
(4)x (2) |
P 12Q
1a
5x2 |
|
1998
P10 |
1989
P11 |
1990
P12 |
|
1 Window glass |
15 sheets |
15.55 |
15.86 |
16.21 |
233.25 |
237.90 |
243.15 |
|
2 Fluorescent tube |
130 boxes |
39.17 |
39.81 |
40.55 |
5.092.1 |
5.175.3 |
5.271.5 |
|
3 Floor detergent |
290 cans |
21.95 |
23.55 |
24.90 |
6.365.5 |
6.829.5 |
7.221.0 |
|
4 Floor finish |
100 cans |
49.39 |
52.27 |
25.53 |
4.939.0 |
5.227.0 |
5.253.0 |
|
5 Latex interior paint |
175 cans |
11.13 |
11.50 |
11.56 |
1.94.75 |
2.012.5 |
2.023.0 |
|
6 Mop head |
200 pieces |
2.86 |
2.93 |
2.99 |
572.00 |
586.00 |
598.00 |
|
|
|
|
Total |
19.149.6 |
20.068.2 |
20.609.65 |
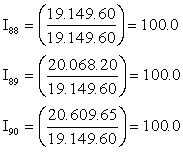
The
schedule of items is the list of items included in the price
index. Often, the schedule of items consists of a sample of all
items of interest, as in the school maintenance supplies
example. Sometimes, it is possible to include all items of
interest in the schedule.
The
price of the Ith item in the schedule in any given
period t is denoted by Pit and the price of this item
in the base period is denoted by Pio. The typical
quantity consume the ith item is denoted by Qia where
the subscript a stands for an average or typical period. These
quantities are used as weights to reflect the importance of each
item.
The
method of weighted aggregates compares the cost of the typical
quantities period t prices with the cost of the same quantities
at base period prices.
The cost at period t prices is:
Cost at period t prices =
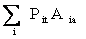
Where the summation is over all the items in the schedule. The cost at base period price is :
Cost at period 0 prices =
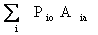
The
price index for period t by the method of weighted
aggregates is the ratio of these two costs, expressed as a
percent. The price index for period t will be denoted by
1it.
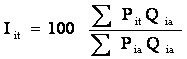
Where:
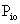 is
the unit price of the ith item in period o (based period). is
the unit price of the ith item in period o (based period).
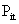 is
the unit price of the ith item in period t (given period). is
the unit price of the ith item in period t (given period).
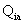 is
the quantity weight assigned to the ith item is
the quantity weight assigned to the ith item
Example
For
the schools maintenance supplies example, the price index series
for 1988, 1989, and 1990 is calculated by the method of weighted
aggregates. Columns 6. 7 and 8 contain the costs of the typical
quantities at the prices of each year. For example, the cost of
15 sheets of window glass at 1988 prices is 15(15.55) = 233.25
while at 1989 prices the cost is 15(15.86) = 237.90. The
aggregate costs of the schedule of items at the prices of the
three periods are shown at the bottoms of columns 6, 7, and 8,
respectively. The index numbers are calculated at the bottom of
the table.
Since the same items and quantities are priced in each period,
the differences in the index are attributable wholly to changes
in the prices of the items. Thus, the price index I89
= 104.8 indicates that the prices of school maintenance
supplies increased, in terms of their aggregate effect, by 4.8
percent between 1988 and 1989. Since the index for 1990 (I90
= 107.6) is above the index for 1989 (I89
= 104.8), the prices, in their aggregate effect, increased still
more between 1989 and 1990. We calculate the percent price
increase between 1989 and 1990 by expressing the percent point
change, 107.6 - 104.8 = 2.8, as a percent of the 1989 index and
obtain 100 (2.8/104.8) = 2.7 percent as the relative price
increase between 1989 and 1990.
Comments
1.
Just as with percent relatives, the
proportional magnitudes of the index numbers in the Table are
not affected by which period is chosen as the base period.
2.
The period from which the quantity weights
are derived is called the weight period. The base period for the
price index and the weight period need not coincide.
3.
When the typical quantity weights Qit
are the quantities consumed in the base period - that is, Qot
the weighted aggregates price index is called a Laspeyres price
index. |
|
8.2 Price Index by Method of Weighted Average
of Relatives
A
second method of compiling a price index series is the method of
weighted average of relatives.
This method utilizes the percent relatives of the prices for
the item in the schedule. The index for period t is simply a
weighted average of the percent relatives for all schedule
items. The weights required by this method are value weights
rather than quantity weights. We shall denote the value weight
for the Ith item by Via.
The
price index it for period t calculated by the method of weighted
average of relatives is

Where:
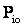 is
the unit price of the ith item in period o (based
period). is
the unit price of the ith item in period o (based
period).
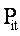 is
the unit price of the ith item in period t (given
period). is
the unit price of the ith item in period t (given
period).
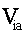 is
the value weight assigned to ith item. is
the value weight assigned to ith item.
The
value weights Via are dollar values that reflect the
importance of each item in the schedule.
For example, the value weights may be obtained from the typical
quantities consumed, Qia by multiplying these
quantities by typical prices.
Example
For
the school maintenance supplies example, we shall calculate a
price index series by the method of weighted average of
relatives with base period 1988. The value weights will be based
on the typical quantities and the unit prices for the base
period 1988 in the Table that is:
Via = Pio Qia
The
necessary calculations are tabulated below. Column 1 in the
Table repeats the schedule of Items, and column 2 contains the
value weights as obtained from the Table. For example, the value
weight for window glass is Via = Pio Qia
= 15.55(15) = 233.25. The sum of the value weight is
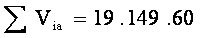
Columns 3, 4, and 5 contain the percent relatives for the prices
of each schedule Item in the three years based on the data in
the Table. Note that all percent relatives are expressed on a
1988 base because the price index is to have 1988 as the base
period. For example, the 1989 percent relative for window glass
is 100(15.86/15.55) = 101.99.
We
now take a weighed average of the percent relatives for each
year. The weighting is done in columns 6, 7, and 8, and the
indexes are obtained at the bottom of the table. The index I89
= 104.8 for 1989 indicates that prices of school maintenance
supplies increased, in terms of their aggregate effect, by 4.8
percent between 1988 and 1989.
Comment
The
price indexes in Tables 26.2 and 26.3 are identical. This
happened because we used base year prices P10,
in obtaining the value weights. In that case, the method of
weighted average of relatives index (26.4) reduces to the method
of weighted aggregates index (26.3) as follows:
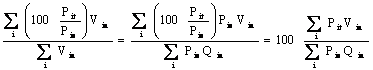
When
prices other than base period prices are used for obtaining the
value weights Via, the two methods will not lead to
identical results. Generally, though, the differences in the
indexes calculated by the two methods will not be great.
We
now take up several considerations that arise in compiling index
numbers series. |
|
8.3 Considerations in Compiling Index Series
Choice of Base Period:
We now take up several considerations that arise in compiling
index numbers series. Any period within the coverage of the
index series can be used as the base period. Of course, when a
special-purpose index is designed to measure price changes
occurring since particular period, such as since the lifting of
price controls, that period would be taken as the base period.
Whenever possible, the base period should involve relatively
normally standard conditions, because many index users assume
that the base period represent, such conditions. Sometimes an
interval of two or more years is selected as the base period. In
this case, the index numbers are calculated so that the indexes
for the base period year average to 100. The base period is then
reported in a form such as 1990-1991 = 100.
Calculation of price index series by method of weighted
average of relatives-school maintenance supplies example
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
|
Schedule of Items |
Value Weight
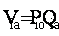 |
Unit Price |
Percent Relative x Value Weight |
|
1998
 |
1989
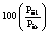
|
1990
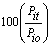
|
1998
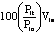
(3)x(2) |
1989
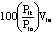
(4)x(2) |
1990
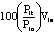
(5)x(2) |
|
Window glass |
233.25 |
100.0 |
101.99 |
104.24 |
23.325 |
23.789 |
24.314 |
|
Fluorescent tube |
5.092.10 |
100.0 |
101.63 |
103.52 |
509.210 |
517.510 |
527.134 |
|
Floor detergent |
60365.5 |
100.0 |
107.29 |
113.44 |
636.550 |
682.954 |
722.102 |
|
Floor finish |
4.939.00 |
100.0 |
105.83 |
106.36 |
493.900 |
522.694 |
525.312 |
|
Latex interior paint |
1.947.75 |
100.0 |
103.32 |
103.86 |
194.775 |
201.242 |
202.293 |
|
Mop head |
572.00 |
100.0 |
102.45 |
104.55 |
57.200 |
58.601 |
59.803 |
|
|
19.149.6 |
|
|
Total |
1914.96 |
2.006.79 |
2.060.958 |
| |
|
|
|
|
|
|
|
|
|
|
|
Shifting of Base Period
Sometimes it is necessary to shift the base period of an index
series that is already compiled, as when two index series on
different base periods need to be placed on a common base period
to facilitate comparison. Usually it is not possible to
recalculate a published index on the new base period because the
needed data are not available. A shortcut method can be
employed; however, that does not entail recalculation of the
index.
To
illustrate the shortcut procedure, let us consider the following
price index series with 1989 as the base period:
|
|
Year |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Price Index (1989 = 100): |
75 |
88 |
92 |
100 |
110 |
122 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Suppose the base period is to be shifted to 1986. We simply divide each index number by 0.75, the index
number for the new base period in decimal form. The index number
for 1986 becomes 75/0.75 = 100.0, that for 1987 becomes
88/0.75 = 117.3, and so on. The new price index series with base
period 1986 is:
|
|
Year |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
|
Price Index (1986 = 100): |
100.0 |
117.3 |
122.7 |
133.3 |
146.7 |
162.7 |
Because the proportional magnitudes of the index numbers are not
affected by this shifting, the new series conveys the same
information about year-to-year relative price changes as the
original series.
The
shortcut procedure yields results identical to those obtained by
recalculating the index series on the new base period when the
index series is calculated by the method of weighted aggregates
with fixed quantity weights. With most other formulas, however,
the shortcut procedure only provides approximate results.
Splicing
When
an index series is revised, the new series can be joined or
spliced to the older series to yield a single continuous series
by a procedure similar to that just described for shifting the
base period of an index series. Suppose the following two price index
series are to be joined:
|
Year |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
|
Old Series
(1983 = 100) |
100 |
103 |
106 |
113 |
130 |
|
|
|
|
|
Revised Series
(1987 = 100) |
|
|
|
100 |
120 |
126 |
131 |
134 |
To
splice the two series together, we simply shift the level of one
of the series so that both have a common value for 1987.
For instance, to obtain a combined series with 1983 as the
base period, we multiply every index in the revised series by
1.30. The spliced series is:
|
Year |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
|
Spliced Series (1983 = 100): |
100 |
103 |
106 |
113 |
130 |
156 |
164 |
170 |
174 |
Collection of Price
and Quantity Data
All
of the data-collection methods discussed is used in collecting
data for price indexes.
Price and quantity data are obtained by observation,
interview, and self- enumeration. Often sampling is used, as in
the consumer price index where probability samples of retail
outlets and of items carried by the selected outlets are
employed to obtain price data. Sampling is also used for the
consumer price index in periodic consumer expenditures surveys
to obtain quantity data for weights.
In
collecting price data for an item over a period of years, it is
important that the quality and other price-determining
characteristics be held as constant as possible. This typically
requires that detailed specifications be developed and adhered
to in pricing the item. Here if is an Example of such a
specification:
Interior latex paint. Professional - or commercial - grade latex
interior house paint, matte or flat finish off white, first -
line or quality.
Note
that color, finish, and quality are specified because each of
these characteristics can affect the price.
A
different problem in collecting price data in ongoing index
series is the adjustment for quality changes in the items
covered by the index. In principle, a price change that is
caused by a quality change should not be reflected in the price
index. In practice, minor quality changes are ignored. On the
other hand, attempts are made in better price indexes to adjust
for important quality changes. However, the conceptual and
measurement problems are difficult. For instance, if an oven
door is modified by the manufacturer to exclude the glass window
while the list price remains unchanged, should this be treated
as a price increase and reflected in the index? If so, what
should be the magnitude of the imputed increase? Extensive
research has been undertaken on how problems connected with
quality changes should be handled.
Another issue in compiling an index series concerns weights. In
some indexes, the schedule includes all or almost all of the
items used in the activity.
For instance, in a price index for highway construction, where a
relatively small number of major items account for most of the
total cost, it suffices for practical purposes to limit the
schedule to these major items. Here, each weight reflects the
importance of the particular item.
Often, however, the schedule must be limited to a sample of
items, since thousands of items may be involved in the activity
and it is neither feasible nor necessary to include them all.
Each item is then selected for the schedule to represent a class
of related items. In such cases, the weight for an item normally
reflects the importance of the entire class represented by the
item.
Consider, for instance, a particular type of insulation that was
selected for a price index for residential building construction
to represent all types of insulation and vapor barriers. The
weight for the insulation the schedule here needs to represent
the importance of the entire class of insulation and vapor
barriers.
Maintenance of Price
Index Series
A
key issue in the maintenance of price index series involves
changes in the items included in the index and in the weights
assigned to the items to keep them up to date.
Should the schedule of items and the weights be changed
frequently so that they are always up to date or should they be
held fixed over a relatively long sequence of years? If
frequent changes are made, changes in the price index series
over time will reflect both changes in price, and changes in the
composition of the index. Another disadvantage of
frequent revision is that it may be very expensive. On the other
hand an index can become badly outdated if the schedule of items
and the weights are held fixed over too long a period.
The
procedure generally followed in practice is to hold the schedule
of items and the weights essentially fixed for 5 to 10 years and
then to revise them. The schedule and weights need not be held
exactly fixed, since procedures are available for making inter
adjustments without disturbing the index. For instance, a new
item can be substituted for an item that has been taken off the
market. And seasonal items, such as fresh produce, can be
included in the schedule in season.
In
addition to periodic updating of the schedule of items and the
weights, revisions often also include upgrading of data
collection and data handling procedures and modernizing of
definitions. A new series of index numbers is then initiated
with each revision.
The new series can be joined to the preceding series, if
desired, by the splicing procedure already explained. |
|
8.4 Uses of Price Indexes
Price indexes play important roles in a variety of applications.
We now consider two important uses of price indexes.
Measuring Real Earnings
As
prices change, so does the quantity of goods and services that
can be purchased by a fixed sum of money. In economic analysis,
it is frequently important to measure change in real earnings
(that is, in the quantity of goods and services that can be
purchased). Price indexes are a basic tool in making this
measurement.
Example: Weekly Earnings
Average weekly dollar earnings of production or non-supervisory
workers on non-agricultural payrolls in the United States during
the period 1985-1989 are shown in the Table below. These
earnings data are expressed in current dollars. For
example, 1985 earnings are expressed in terms of the buying
power of workers' dollars in 1985, and earnings in 1986 are
expressed in terms of the buying power of workers' dollars in
1986. We see that earnings in current dollars increased steadily
during the period.
The
extent to which the prices of goods and services purchased for
daily living by the workers and their dependents changed during
the period is shown in column 2 by the consumer price index for
urban wage earners and clerical workers. This index is expressed
on a 1985 base period in the table. Note that prices in 1986
stood at 101.6 percent of their 1985 level. Thus, on the
average, families had to spend $1.016 in 1986 for every $1 spent
in 1985 in purchasing goods and services for daily living.
Consequently, the average weekly earnings of $304.85 in 1986
were equivalent in purchasing power to 304.85/1.016 = $300.05 at
1985 prices. Since 1985 average weekly earnings were $299.09, we
see that most of the increase in average weekly earnings between
1985 and 1986 (from $299.09 to $304.85) was offset by price
increases and that real earnings increased only slightly.
Earnings in current and 1985 dollars - weekly earnings Example
|
Year |
(1) |
(2) |
(3) |
(4) |
(5) |
|
Weekly Earnings |
Consumer Price Index
(1985=100) |
Weekly Earnings in 1985 Dollars
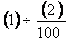 |
Relatives for Column 3 |
|
Link Relative |
Percent Relative (1985=100) |
|
1985
1986
1987
1988
1989 |
299.09
304.85
312.50
322.36
335.20 |
100.0
101.6
105.2
109.4
114.7 |
299.09
300.05
297.05
394.66
292.24 |
-
100.3
99.0
99.2
99.2 |
100.0
100.3
99.3
98.5
97.7 |
| |
|
|
|
|
|
|
Sourrc:
Basic data from Monthly Labor Review
The
average weekly earnings in the other years at 1985 prices are
obtained by the same procedure: Each current earnings figure is
divided by the decimal value of the price index for that year.
Column 3 of the Table contains the average weekly earnings data
expressed at 1985 prices. These data are said to be in constant
dollars or 1985 dollars since they are expressed in terms of the
purchasing power of the dollar in 1985. Relative changes in
constant-dollars earnings indicate the relative changes in
purchasing power associated with the money earnings - that is,
the relative changes in real earnings. To show these relative
changes explicitly, we have expressed the constant - dollars
data as link relatives in column 4 in the Table and as percent
relatives in column 5 with 1985 = 100. The link relatives show
that real earnings increased slightly between 1985 and 1986 and
then declined a little each year between 1986 and 1989. The
percent relatives show that real earnings in 1989 were only at
97.7 percent of their 1985 level.
Comment
We
noted earlier that proportional magnitudes in an index series
are not affected by the choice of the base period but that the
absolute magnitudes are affected. The same holds for constant –
dollars series. Thus, in the weekly earnings example, if the
consumer price index had been expressed on a 1989 base, the
constant-dollars earnings would have differed from column 3 of
its Table, but the percent relatives and the link relatives
based on these 1989 constant-dollars data would have remained
exactly the same.
Measuring Quantity Changes
Many
important business and economic series on volume of activity are
expressed in current dollars. Changes in the dollar volume
reflect quantity changes, or price changes; or both. Often,
there is interest in the quantity changes alone.
For example, if retail sales this year are 5 percent higher than
last year's sales, is this due to price increases only or did
the physical volume of goods sold increase? We can measure
relative changes in quantities by the use of price indexes. The
procedure is similar to that for expressing current-dollars
earnings as constant-dollars earnings.
Appliance Sales Example
Annual sales (in $ thousands) by a manufacturer of household
appliances during 1989-1992 are shown in the Table below. A
relevant price index for the products of the manufacturer is
shown in column 2. The constant-dollars sales in 1989 dollars
are shown in column 3. The calculations parallel those for
obtaining constant dollars earnings in the previous Table. The
link relatives and the percent relatives (1989 = 100) of the
constant-dollars sales are shown in columns 4 and 5,
respectively. We see that the quantity of household appliances
sold increased by 33 percent between 1989 and 199 and that the
annual rate of increase was about 10 percent per year.
Manufacturer's sales in current and 1989 dollars appliance
sales Example
|
Year |
(1) |
(2) |
(3) |
(4) |
(5) |
|
Annual Sales ($ thousand) |
Product Price Index
(1989=100) |
Sales in 1989 Dollars($ thousand)
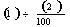 |
Relatives for Column 3 |
|
Link Relative |
Percent Relative (1989=100) |
|
1989
1990
1991
1992 |
38.500
43.538
49.050
54.950 |
100
103
105
107 |
38.500
42.270
46.714
51.355 |
-
109.8
110.5
109.9 |
100.0
109.8
121.3
133.4 |
| |
|
|
|
|
|
|
Comments
1.
When current-dollars series are converted
into constant dollars, the price index must be relevant to the
series. For instance, we would not use a food price index to
adjust a series appliances sale. or the consumer price index to
adjust the sales of a steel manufacturer
2.
When a current-dollars series is converted
into a constant - dollars series, the latter is often refined to
as a deflaled series. |
|
8.5 Quantity Indexes
A
quantity index is a summary measure of relative changes over
time in the quantities set of items -
for
instance, in the quantities of automobiles, trucks, and other
imported annually by the United States. In such index series,
the quantities can from one period to another but the prices or
other weights remain fixed. The index mulas are analogous to
those for price indexes.
The
quantity index It, for period t calculated by the
method of weighted aggregates is
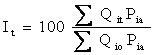
The
quantity index for period t calculated by method of weighted
average of relatives is

A
problem in constructing quantity indexes arises in the choice of
weights.
The usual price or value weights may not be appropriate here.
Consider a company that wishes to measure quantity changes in it
outputs of different electronic circuits assembled purchased
components. Here, price weights or value weights for the
different circuits would reflect mainly the prices or values of
the purchased components and not the quantities of assembly work
performed by the company per se. Weights derived from the
typical number of hours expended in assembling each circuit or
form the value added to each circuit in the assembly would be
more appropriate. Value added here would be the value of the
circuit when shipped from the plant less than the cost of the
purchased components and other purchased goods and services (for
example, fuel, electricity, containers) used in assembling the
circuit and packing it for shipment. The index of industrial
production utilizes value-added weights in many of its segments. |
|
|
|
|